【摘要】：当结构中存在斜杆且与定向滑动支座相连时，若定向滑动支座的链杆方向与杆件轴线方向不同，则可能引起不同的形常数。对于图6-9所示结构，在作单位弯矩图时，斜杆BC可套用一端固定另一端定向滑动的单跨超静定梁，其单位弯矩图如图6-9所示。在作图时，由于不考虑轴向变形，斜杆相当于两端固定的单跨超静定梁，如图6-10所示。位移法典型方程为：求系数和自由项：代入方程求得：由作最终弯矩图，如图6-10所示。
当结构中存在斜杆且与定向滑动支座相连时，若定向滑动支座的链杆方向与杆件轴线方向不同，则可能引起不同的形常数。以图6-9（a）、（b）所示结构为例，当不考虑轴向变形时，两结构均有一个角位移未知量。对于图6-9（a）所示结构，在作单位弯矩图时，斜杆BC可套用一端固定另一端定向滑动的单跨超静定梁，其单位弯矩图如图6-9（c）所示。而对于图6-9（b）所示结构的基本体系，在单位位移
作用下，由于不考虑轴向变形，C点不产生竖向线位移，因此斜杆BC 相当于两端固定的单跨超静定梁，其单位弯矩图如图6-9（d）所示。
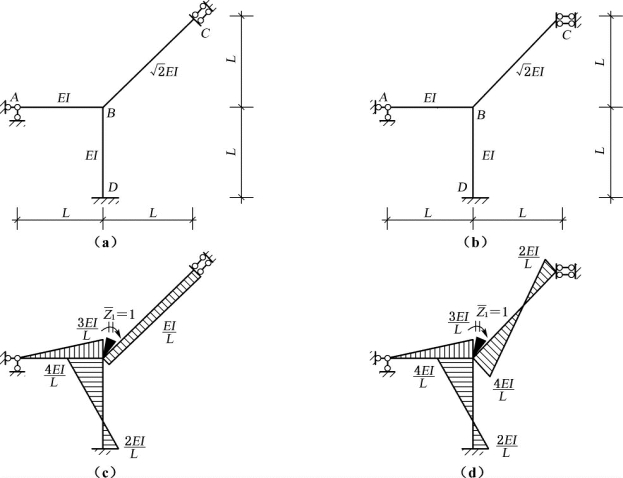
图6-9
【例6-4】 试用位移法求解图6-10（a）所示结构，并作M 图。（西安建筑科技大学2012）
【解】 该结构具有两个基本未知量，且存在局部静定部分，可先对原结构进行简化，如图6-10（b）所示，简化后的基本体系如图6-10（c）所示。在作
图时，由于不考虑轴向变形，斜杆相当于两端固定的单跨超静定梁，如图6-10（d）所示。而在作
图时，斜杆只有平动，不产生弯曲变形，故斜杆无弯矩，如图6-10（e）所示，MP图如图6-10（f）。
位移法典型方程为：
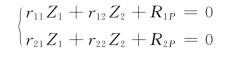(www.xing528.com)
求系数和自由项：
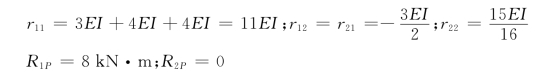
代入方程求得：
由
作最终弯矩图，如图6-10（g）所示。
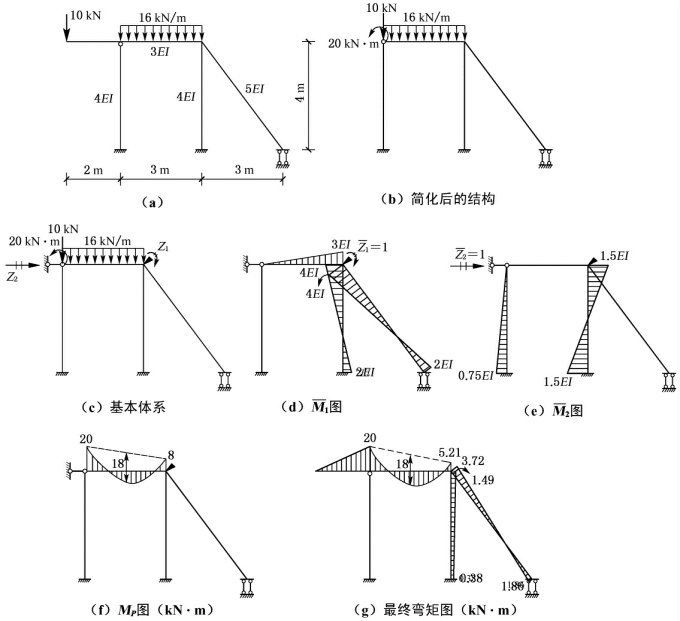
图6-10
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
