用位移法求解结构内力中的无穷杆与弦转角

用位移法求解结构的内力时，常会遇到EI为无穷大的杆件，这种杆件称为无穷杆。无穷杆的存在，会对结构的基本未知量以及单位弯矩图产生一定的影响。例如图6-7（a）所示结构，已知杆AB 的EI为无穷大，其余各杆的EI为常数，其基本未知量为结点D处的竖向位移，故基本体系如图6-7（b）所示，在作基本体系时的单位弯矩图时，由基本体系的变形图6-7（c）可知，BC杆在B处不仅有竖向的单位位移，而且还有转角θ=1／L。同样，对于BD 杆而言，在B处也有转角θ=1／L，称该转角为弦转角，产生的原因是无穷杆发生侧移而不发生弯曲变形，带动与其相连的杆件产生转动（牵连位移），引起附加转角的大小为1／杆长（无穷杆的长度）。基本体系在时的单位弯矩图如图6-7（d）所示。

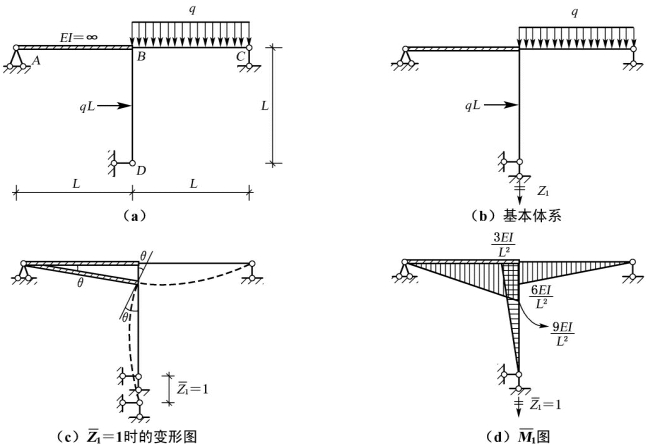
图6-7

【例6-3】　试用位移法计算图6-8（a）所示结构，作出弯矩图，并求CD 杆的剪力。（浙江大学2010）

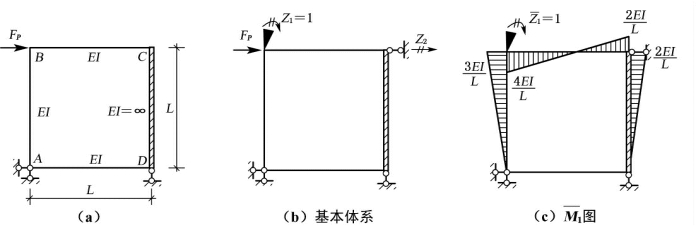
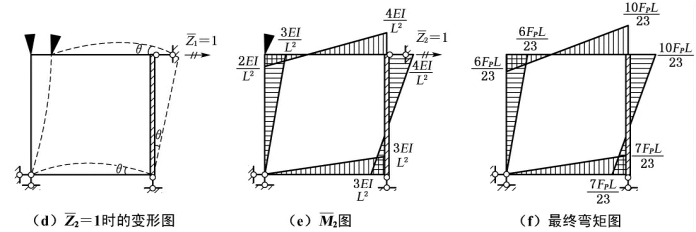
图6-8

【解】　该结构有两个基本未知量，分别为结点B的转角和C的水平位移，基本体系如图6-8（b）所示，作图如图6-8（c）所示。在作M2图时，基本体系在单位位移时的变形图如图6-8（d）所示，BC 杆和AD 杆均有弦转角θ，大小为θ=1／L，故图如图6-8（e）所示。由于荷载作用下不产生基本体系的弯矩，仅产生附加链杆中的支反力，故无MP图。(www.xing528.com)

位移法典型方程为：

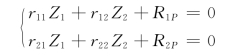
求系数和自由项：

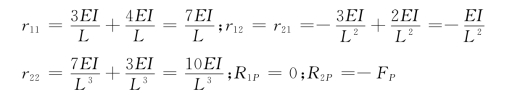
代入方程求得：Z1=FPL2／69EI；Z2=7FPL3／69EI

由叠加作最终弯矩图，如图6-8（f）所示。

由最终弯矩图可知：（正剪力）