如何合理选取基本结构

用力法求解超静定结构时，解除多余约束后所得的静定结构为原结构的基本结构，对于基本结构的选取应注意以下问题：

（1）应选取合理的基本结构使计算过程简化

如在对图5-9所示的结构来用力法求解时，可选图5-10（a）、（b）两种基本结构，但两者的计算量及其单位弯矩图的求解存在很大差异，可以证明，图5-10（b）的基本结构在作单位弯矩图、荷载弯矩图以及图乘时的工作量最少。因此，在解除超静定结构多余约束和选取基本结构时，应使所选基本结构的弯矩图尽量好画，也便于图乘。

图5-9

图5-10

（2）基本体系必须是几何不变体系，避免选成几何可变体系。

如图5-11（a）所示的结构在用力法进行求解时，可选图5-11（b）所示的三铰刚架为基本结构，但图5-11（c）为几何可变体系，不能作为基本结构。

图5-11

（3）在解除多余约束时，若将刚结点改为铰接，要注意基本未知量的个数。

①一个单刚结点改成铰接，解除一个多余约束，未知力为一对等值反向的力偶。如图5-12（a）所示。

②若将一个连接n个刚片的复刚结点改成铰接点，相当于解除了（n-1）个多余约束，应代以（n-1）对等值反向的未知力偶（原因：连接n个刚片的刚结点相当于3（n-1）个约束，将其改为铰接后形成的铰结点相当于2（n-1）个约束，故解除了（n-1）个约束。这些被解除的约束均为限制结点转动的约束，故应代以（n-1）对等值反向的力偶）。如图5-12（b）所示连接三个刚片的复刚结点，在解除多余约束时将刚结点改为铰接，则应在与铰相连的杆端施加两对等值反向的未知力偶。

(www.xing528.com)

图5-12

【例5-4】　图5-13（a）所示的超静定结构，若选图5-13（b）为基本结构，试用力法绘出结构的弯矩图，设各杆的EI 为常量。（同济大学2007）

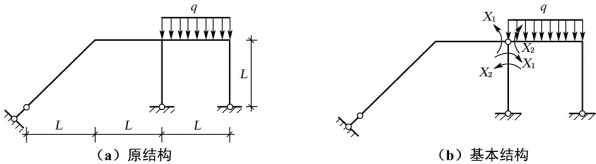
图5-13

【解】　作基本结构的和MP图，分别如图5-14（a）、（b）和（c）所示。

图5-14

建立力法典型方程：

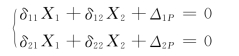
求系数和自由项：

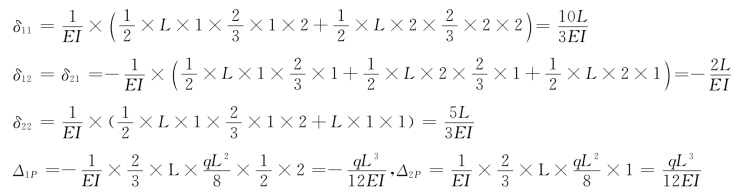
代入方程求得：

由叠加作出最终弯矩图，如图5-14（d）所示。