用力法求解对称的超静定结构时，一般有三种简化分析的方法：①选取对称的基本结构；②取半结构计算分析；③选取成对的未知力。
究竟采用何种方式应根据具体题目而定。在选取半结构分析时，对称轴处的等代支座可根据原结构在外荷载作用下的变形特点合理选取。同时应注意的是，对称结构在支座变位和温度作用下亦可进行简化分析。
【例5-1】 试画出图5-1（a）所示结构分别在正对称和反对称荷载作用下的半结构，已知各杆的EI 为常量。
图5-1
【分析】 原结构在正对称荷载作用下，对称轴处的转角位移和水平位移属反对称位移，故应为零，AB 梁的跨中可简化为定向滑动支座，D 结点简化为固定支座。在反对称荷载作用下，对称轴处的竖向位移为正对称位移，应为零，AB 梁的跨中可简化为活动铰支座，中柱DG 的刚度减半。正对称和反对称半结构分别如图5-1（b）、（c）。
5.超静定结构的位移计算
当采用图乘法进行超静定结构的位移计算时，为避免通过求解超静定结构获得虚拟状态下的单位弯矩图，可将单位荷载施加在原结构的任意一个静定的基本结构上。
【注意】 在进行超静定结构的位移计算时，要关注引起位移的因素有几种，尤其是在计算支座变位引起的超静定结构位移时，不能遗漏支座变位对位移的贡献。
【例5-2】 图5-2所示梁的EI为常量，固定端B发生了向下的支座位移Δ，则由此引起的梁中点C 的竖向位移为（ ）。（浙江大学2007）
A.Δ／ 4（↑） B.Δ／ 2（↓） C.5Δ ／8 （↓） D.11Δ／16（↓）
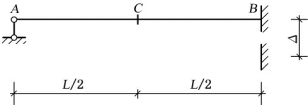
图5-2
【分析】 本题为超静定结构的位移计算问题，先作出结构由于支座变位引起的弯矩图MC图，如图5-3（a）所示。并选取图5-3（b）所示的悬臂梁为原结构的基本结构，在C 处施加单位竖向荷载，作出虚拟状态下的弯矩图。
图5-3
则：
，故选D。
【注意】 本题是超静定结构在支座变位下的位移计算，不仅需采用图5-3（a）、（b）所示的弯矩图进行图乘，还需考虑由于支座变位对C 点竖向位移的贡献。
【例5-3】 图5-4所示结构的支座A 下沉了2cm，已知各杆的抗弯刚度EI=4.02×104kN·m2。试用力法分析作其弯矩图，并求C 点的竖向位移ΔCy。（东南大学2015）
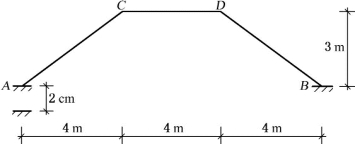
图5-4
【解】 本题为对称结构发生非对称支座变位的问题，可分解成正对称和反对称两种情况进行简化分析，分别如图5-5（a）、（b）所示。
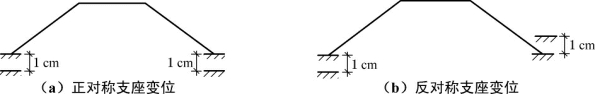(www.xing528.com)
图5-5
（1）在正对称支座变位情况下，结构整体下沉1cm，只发生刚体位移，而不产生弯曲变形，故无弯矩。
（2）在反对称支座变位情况下，取半结构进行分析，如图5-6（a）所示，并选取图5-6（b）为其基本结构，作
图，如图5-6（c）所示。
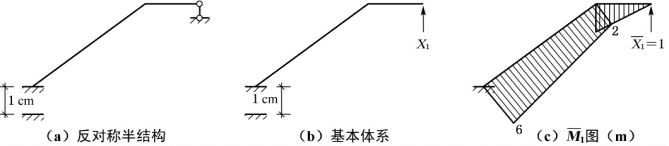
图5-6
建立力法典型方程：δ11X1+Δ1C=0
系数：
；
自由项：
解方程得：X1=4.5kN
叠加得最终弯矩图，如图5-7所示。
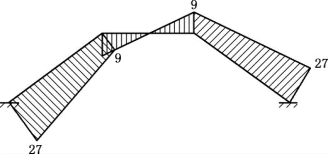
图5-7 最终弯矩图（kN·m）
求C 点的竖向位移：
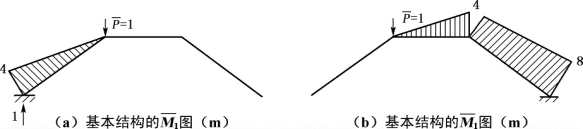
图5-8
①法一：若选取图5-8（a）所示的基本结构，在C点施加竖向单位力，作出虚拟状态下的单位弯矩图。
故有：
②法二：若选取图5-8（b）所示的基本结构，在C点处施加竖向单位力，作出虚拟状态下的单位弯矩图。
故有：
=0.014 8m（↓）
可见，法二无需考虑支座变位的影响，可避免漏项。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
