理论神经信息学初探：记忆提出的不稳定流形

13.12.5.1　混沌轨道记忆

我们提出的理论是：记忆的介质为不稳定混沌轨道。从流形角度看，N维流形中只有一个特征量大于0，是不稳定流形；其他都小于0，是稳定的流形。这一不稳定的流形就是所记忆的内容。

不动点、极限环、连续吸引子本质上是相同的，都以稳定吸引子为基础。而不稳定轨道作为记忆却是以不稳定流形为基础的。混沌轨道的记忆符合S 空间理论，S 空间中都是以神经脉冲序列为基本单元的。

从图13.4（与图2.50接近）所示的系统可见，任意初值R 都会随着时间的延长，逐渐向不稳定流形（R′）靠近。若系统是线性的，则R′一定沿着直线趋向无穷，这就没有意义；而对于非线性系统，特别是混沌系统，不稳定流形在有限空间内会不断弯曲，如图13.5所示。从图13.4可以看出，从任意的初值R 出发，最后都会趋向不稳定流形输出，而这一不稳定流形的轨道取决于系统参数。如果这一混沌系统的轨道是可以排序的，则此系统可以实现定量化的存储。这与现有的定性记忆模型有着本质区别（补充说明：不熟悉非线性动力学的读者可能会有误解：如何在神经系统中找到混沌轨道？其实在脑中混沌轨道是以神经脉冲序列的形式表现出来的）。

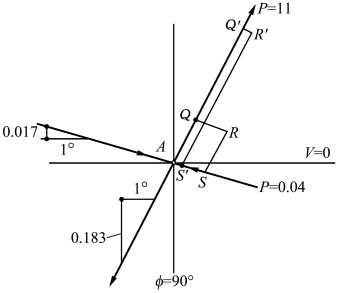
图13.4　带有稳定和不稳定流形的系统示意

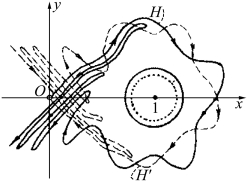
图13.5　混沌系统中的不稳定流形(www.xing528.com)

Hopfield 的人工神经网络模型主要考虑了利用突触连接强度的变化来实现学习、记忆和信号处理。当H-H 方程的圆映射都是单调递增圆映射时，图13.6就是图6.6，它可得方程（6-9），方程里的aij就是连接强度，aij的不同决定哪些流形是否稳定。如果只保留一个分量的流形不稳定，这个不稳定流形就是作为记忆的信息，由此就可得到图13.6所示的记忆回路。

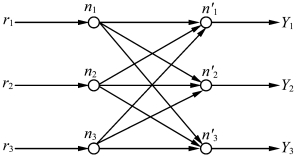
图13.6　记忆回路

13.12.5.2　新记忆模型的神经回路

要将不稳定流形作为记忆很容易。图13.6这样3×2 的神经网络可以用一矩阵来表示［见式（6-11）］，只要改变连接强度，使矩阵的某一个特征量大于0，就有了一个不稳定流形。这种不稳定流形的形状（轨道）由系统参数确定。如果系统参数不变，则输出的不稳定流形也是一定的。

这种记忆器的输入（刺激）信号是r1、r2、r3，而且这三个输入量可以任意组合，也可以只输入任意一个作为刺激。一旦输入停止，系统就会沿着不稳定轨道不断运动，这就是记忆的输出。由于该系统中只有一个不稳定流形，因此无论刺激如何，系统最后都会沿着不稳定流形（相当于图13.5中那样）运动。这个轨道的不稳定表现在Y1、Y2、Y3 的变化上。除了3×2 网络，也可用4×2 网络及其他很多网络实现不稳定流形记忆。网络结构可以自由构成，符合简并原理即可。记忆输出可以不是Y1、Y2、Y3 中的一个输出，而是很多组合输出（见图13.6），实际上高维轨道输出也可以作为记忆输出，图13.6中的Y1、Y2、Y3 就是高维轨道的分量。这些输出从数学上看，应该像矩阵输出，从回路上看，也像阵列谱输出。如果这些输出与视觉的阵列谱一致，那便是图像的存储。同样也可以是嗅觉或听觉的阵列谱的记忆。

图13.6的记忆回路和图6.5的计算回路实际上是一样的。记忆的数学模型和运算模型也是相近的，可能都是矩阵形式（是否是矩阵形式还需进一步讨论，见第6 章），记忆仅仅改变了系统的一些参数。根据S 空间理论，在不改变单调性的条件下，系统任意的参数变化不会影响系统的输出结果。也就是说，系统记忆了一些信息，但这些信息不会影响系统的运算功能。根据这种猜测，脑中的记忆可能与运算系统并在一起（至少在某些地方会合在一起），而并不像计算机那样，把记忆存储在一个特定的区域内。