生物声呐与L效应的定义

如图11.1所示为产生L 效应的网络。其中o 信号要传输到c 所在的通路中，首先要经过N1 使信号变为a，a 本身频率较低（小于ωc），它是第二类神经脉冲序列。a 通过神经元N2 后，输出c 不可能保持与a 相同的排序规律，此时可以认为有用的神经信息到a 处为止，以后的信号c 实际上已成为噪声。a 的信号要延伸下去，只有使c 信号具有与a 相同的排序性，才能说a信号传递到了c 信号处。

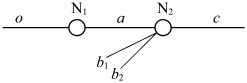
图11.1　产生L 效应的网络

能否利用外界因素使c 信号与o 有同样的排序规律？办法有很多，为讨论方便，凡是能使第二类脉冲序列提升为第一类脉冲序列的效应称为L 效应。例如图11．1中，a 信号与b1，b2 合成后，脉冲序列的频率大于N2 所需的阈值频率ωc，成为一类脉冲序列。

更明确地说，L 效应最基本的作用是使第二类脉冲序列a 在神经回路中变为第一类脉冲序列。第二类脉冲序列本身具有可排序性，但是这一脉冲序列本身频率已经低于阈值ωc，所以它再经过一个细胞后就成为噪声了。L效应就是加上外界因素可以使神经元N2 的输入脉冲序列a 的频率超过阈值频率ωc，使输入脉冲序列a 处在第一类状态。要做到这一点，可以从两个方面进行考虑：一是降低ωc，使信号a 的频率大于ωc；二是提高a 的频率，这样也可使a 成为第一类脉冲序列。要实现这两点可以有很多手段，虽然我们还没有完全掌握，但是可以给出一些可能的方法。

（1）首先看H-H 方程中的Ioffset这一项，它是非门控离子电流。它与外界环境有关，外界离子浓度变化会引起Ioffset变化，而它的变化可以引起细胞的ωc 变化（见第5 章）。也就是说，外界环境变化可以使a 由第二类神经脉冲序列变为第一类脉冲序列。

（2）改变N1 与前一神经元连接处的连接强度（见图11．1）可以改变a的频率。而细胞间的突触处连接强度也可受周围环境影响而变化，最明显的是突触周围的胶质细胞的变化（见第3 章）。(www.xing528.com)

（3）从图5.8、图5.9等可以看出，改变离子通道的参数与改变输入脉冲信号频率是等效的。而神经元N1 和N2（见图11.1）中离子通道参数的变化也与环境有关，这也表明环境可通过改变离子通道来改变ωc。神经元周围存在大量的胶质细胞，它们的活动也可大大改变神经元所处的环境，从而使神经元的输出脉冲频率产生变化，使输出c 成为第二类神经脉冲序列，也即使a 成为第一类神经脉冲序列（见图11.1），起到L 效应作用。

（4）在图11.1所示的系统中加入噪声b 能使输出信号c 与a 具有相同的单调关系吗？在一定条件下是可以的。根据我们的计算，如果加入信号不变的脉冲序列b1，b2，则针对在一个特定的频段内的a，可以使c 与a 具有同样的排序性。从信息研究的角度来看，加入b1，b2 相当于调整放大器的“零点”。

接下来要问，什么样的信号是不变的信号？最简单的是等周期的脉冲序列，但在脑中存在等周期脉冲序列吗？还是用计算来说明。对一个神经元输入等周期脉冲序列，输入脉冲序列的频率（周期）为一系列由高到低的数值，由此得出一系列不同频率的输出脉冲序列。我们发现，高频脉冲序列通过神经元后，输出的脉冲序列频率总是降低，而且输入脉冲序列的频率越高，输出脉冲序列的频率下降越快。但当输入脉冲序列的频率低到一定值时（假定为ωd2），输出脉冲序列的频率反而会升高。如果输入脉冲序列的频率在ωd1（ωd1＞ωd2，）处，输出脉冲序列的频率是下降的，如果输入信号可以从ωd1连续变到ωd2，则在这两个频率之间一定会存在一个稳定的输出。这样的脉冲序列正好可用作为图11.1的噪声b。当输入脉冲序列的频率更低，如远低于ωd2，输出脉冲序列的频率则不会升高，如果认为稳定的噪声的频率太低，则可加入b1，b2 两路噪声。有一段时间，有很多文献讨论脑内存在40Hz的电波［4］，不知这是否与这里的讨论有关。

图11.1中，如果要让加入的噪声b 随着o 一起变化（b 与o 保持相同的递增或递减关系），这里的噪声信号b 需要是来自诸多噪声ei 的叠加信号（同源噪声网络见图11．2）。同源噪声e 的单调性与输入信号r 相同，e 信号与a 来自同一信号源（如是同一神经元的发放信号，或a 是来自感受细胞的信号，e 是来自同一感觉器官的其他感受细胞的信号等），称这些噪声e 为“同源噪声”。系统加入同源噪声后也可保证图11．1和图11．2中信号c 能与a 具有相同的单调性。

由于脑的复杂性和神经网络的复杂性，各种情况都会产生，以上讨论的诸多因素也可能同时起作用，使信号a 成为第一类脉冲序列，从而使信号c能与a 有同样的单调性变化。