假设外界一维图像光线成像在一维细胞阵列上,光线在细胞阵列光强分布满足G(xn)规律,G(xn)=e1,e2,…,ep。式中,p 表示第p 个细胞,原来第p 个双极细胞感受信号是ep,但细胞p 还受左右两边细胞的侧抑制作用影响。这里先假定左右两边各有三个细胞对其产生影响,抑制规律按K(n)规律变化。那么对双极细胞p 实际得到的输入可以理解为

这里的γp 可看作第p 个双极细胞实际输入的信号大小,由于我们已经知道神经细胞输入和输出的单调性都是一致的,所以在这里按S 空间理论也可将γp 理解为双极细胞p 的输出。
如果把离散的系统变为连续系统,则可以将方程中带有∑的一项更一般化:
![]()
这里m 变为连续的x,x 是阵列谱的空间位置,同样n 变为τ,τ 是空间的位移,最后双极细胞阵列输出应该是(https://www.xing528.com)
![]()
式(10-5)与式(10-7)并不完全正确,因为侧抑制引起的影响不一定是“减法”,也可能是改变连接强度,这就变为“乘法”。不管是减还是乘,总之侧抑制起到减弱作用,因此用式(10-7)来理解侧抑制还是有效的。
视觉侧抑制已经被广泛用于图像处理,它可使图像轮廓清晰。侧抑制的效果如图10.11 所示。其中,ξ(x)表示式(10-7)中Q、G、H 等项的大小,它是x 的函数。它的基本原理是,当看到一个类似黑色线条波形G(x)这一类不太陡的“山坡”时,如果我们能找到一个K(·),使它按式(10-6)进行卷积,产生虚线所示的把较为平坦的波形G(x)变换成一个很陡峭的山峰Q(x),那么这可用来增强图像轮廓的清晰度。这一原理已经广泛应用在图像处理中。文献[5]中列出了很多种K(·)函数。
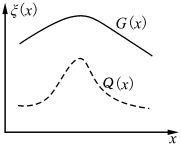
图10.11 侧抑制的效果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




