非线性科学中的相似性例子

9.3.1.1　元胞自动机中的相似原理

元胞自动机中存在很多相似之处，可以在任何的二维元胞自动机的图形中看到局部图形之间存在的很多相似性（很多相似三角形），图9.5所示的元胞自动机仅仅是其中一个例子。

图9.5　元胞自动机中有很多局部相似之处

9.3.1.2　分形图中的相似原理

分形图形展示了各种相似性：科赫曲线（Koch curve，见图9.6）、芒德布罗集（Mandelbrot set，见图9.7）和谢尔平斯基镂垫（Sierpinski gasket，见图9.8）都展示了局部与整体的相似性等。这些图形都是按某种简单规律重复作用而形成的。

图9.8　谢尔平斯基镂垫

图9.7　芒德布罗集(www.xing528.com)

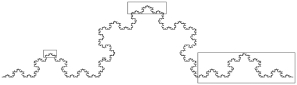
图9.6　科赫曲线

9.3.1.3　迭代系统中的相似原理

不管是什么单峰映射函数，都存在相近的分岔图，如图9.9所示为一例单峰映射的分岔。在分岔图中存在很多相似之处，而且都存在不变的费根鲍姆数。

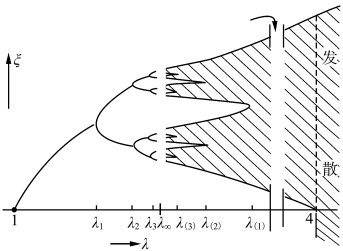
图9.9　单峰映射的分岔

重整化群方法特别适用于研究一个系统在测度变化下的不变性，这种不变性通常意味着这个系统中存在某种分形结构，而重整化群方程提供建立在这种分形结构上的分析工具。分形结构中存在局部与整体相似性。重整化群理论被广泛承认，说明物理系统中存在大量的相似性。

从以上这些例子中可以得出一个规律：任何用同一规律重复作用所产生的图形或结构都具有嵌套和相似性结构。