【摘要】：有趣的是，Jeffress的双耳时差模型也被包括在内。不管Jeffress 模型是否存在缺点，至少此模型被很多生物学家所承认，经过了近七十年还在对其进行研究，而且有文献说该模型有生物学根据［13-14］。有意思的是针对同一回路，有两种不同解释：Jeffress 模型要求神经元之间的连接长度不能随便改变，因为连接长度变化，将直接影响一致性监测细胞的工作状态。同时，按简并模型解释的系统灵敏度和可靠性（冗余度）都远远高于Jeffress 模型。
图9．1完全是按照理论画出的回路，按同样的规律还可以画出很多类似的图，这种种变异的回路应该都能满足测定方向的功能。有趣的是，Jeffress的双耳时差模型也被包括在内。
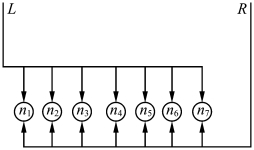
如果把图9．1中大部分细胞都去掉，只留下n1，n′1以及h8，h9，h10，h11，h12，h13，h14，这就是近七十年来被大家广泛承认的Jeffress 模型（见图9．2）［12］。不管Jeffress 模型是否存在缺点，至少此模型被很多生物学家所承认，经过了近七十年还在对其进行研究，而且有文献说该模型有生物学根据［13-14］。这是否代表简并回路也是符合生物实际的？有意思的是针对同一回路，有两种不同解释：Jeffress 模型要求神经元之间的连接长度不能随便改变，因为连接长度变化，将直接影响一致性监测细胞的工作状态。而简并模型解释，细胞工作状态与长度无关，也与回路结构变化无关，不用考虑连接长度。同时，按简并模型解释的系统灵敏度和可靠性（冗余度）都远远高于Jeffress 模型。应该说，根据简并模型得到的解释更符合生物实际。
(www.xing528.com)
图9.2 Jefferess 的双耳时差模型
通过这一例子可以看到，用不同原理去分析和理解同一神经网络，所得的结果也会有很大差距，这种情况会在很多神经回路中碰到。不理解神经系统中存在简并性，往往会出现其他的分析方法和对神经系统的另一理解。这一现象值得我们思考。有人说眼见为实，其实对这个“实”还要仔细分析，通常对理解了的东西才能有更好的认识。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
