变频多普勒效应计算：生物声呐及感觉系统信息处理机理研究

上述讨论的是单纯音的多普勒效应，这是按物理定义的多普勒效应来分析的。实际上，蝙蝠等发出的声波或飞行目标物（如小飞虫）发出或反射的声波都不是单纯音，可以很复杂，可以是多种频率叠加的声波，也可以是按时间变化的声音，现在先对随时间频率变化的多普勒效应进行分析（或称变频多普勒效应），同样的神经回路还能进行测量吗？神经系统确实是采用了同样简单的策略。

仔细分析多普勒效应，如以主动声呐为例，不管声音频率是高是低，当物体运动时，它对不同频率的声音都是按同样方向增加或减少反射频率的。耳朵把声音转换为脉冲序列，声音在幅值不变、频率增加的情况下，转换成的神经脉冲序列的频率也增加。变频的声音信号变为神经脉冲序列，这一脉冲序列的频率也随时间变化。由于多普勒效应对所有频率变化规律都是单向变化的，这也表明原有的脉冲序列的频率曲线经多普勒效应变化后对应的脉冲序列的频率曲线与原曲线近似呈平移关系，因此运动前后的两串脉冲序列是符合S 空间中脉冲序列排序规律的。广义圆映射中的定理5.1 正好可以用来分析变频的多普勒效应。采用广义圆映射取两串符号序列，根据两串符号序列求出它们之间的距离，距离可以用来反映变频多普勒效应的大小。

下面采用计算机仿真来证明。为不失一般性，采用频率连续增加和减少的脉冲序列作为输入信号。假定频率随时间的变化规律如正弦函数的最后1／4 周期，变化范围为300Hz，当起始频率为500Hz 时，相应的变化函数为

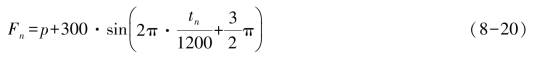
式中，Fn 为tn 时刻的频率，p 为基线频率，这里p=800Hz，tn 范围为0～300ms。当t0=0 时，起始频率F0=500Hz。当起始频率加上一个Δ 时，则相应的所有Fn 都加上该Δ。

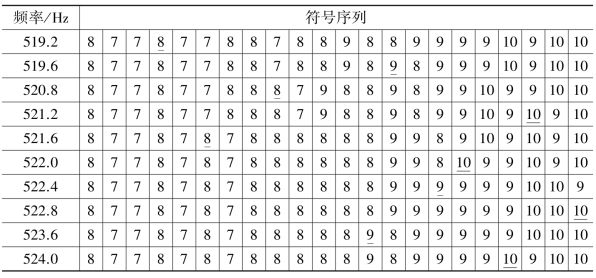
从表8.3可以看出，变频多普勒效应也与符号序列呈单调关系。按广义的距离定义，也可以得出与等周期多普勒效应一样的效果。

表8.3中所示的是精细的分析，不涉及任何统计的规律。只要神经方程能定性地反映神经元的电生理过程，其结果应该是相当可信的，因为推理所用的理论是成熟的圆映射和符号动力学理论。

表8.3　不同的起始频率F0 的脉冲序列与输出脉冲序列的符号序列关系(www.xing528.com)

续表

由以上分析可知，一个神经脉冲序列只需要十几个神经脉冲就能够达到0.01Hz 的分辨率，而神经元输出十几个脉冲的时间仅需几十毫秒。脉冲数越多，测量分辨率越高，时间略增长；若降低分辨率，则检测速度可加快。由此分析，神经系统是有能力分辨双耳多普勒效应的。

需要指出的是，本书只说明神经系统有极高的分辨率（或称灵敏度），但是没有讨论测量绝对精度。本书讨论的“定量”，是在S 空间中的定量。虽然进行的是纯粹理论上的探测，但能证明神经系统是有能力达到这样高灵敏度的检测水平。

只有认识到存在“精细”与“定量”编码的机制，才有可能考虑到双耳多普勒效应之类的现象存在，这对了解海豚等生物声呐是有益的。