【摘要】:神经系统中每一神经元不仅可以做数量运算,而且可以做逻辑运算。图6.8逻辑“或门”3.“非门”在神经系统中“非门”就是抑制性神经元。4.多输入“与或门”在神经系统中还有一种如图6.9所示的特殊逻辑。图6.9多输入“与或门”以上种种逻辑关系在H-H 方程中是很容易表达的,只要调节连接强度、神经元参数,保证输入一定数量的脉冲后一个神经元能输出一个脉冲,就可以表示上述几个逻辑关系。
神经系统中每一神经元不仅可以做数量运算,而且可以做逻辑运算。这种逻辑变化规律在文献中实际上早就有了,如文献[17]。下面按理论系统整理一下。
1.“与门”与多输入“与门”
如图6.7所示,当r1 与r2 脉冲同时输入时,神经元就有一个脉冲rc 输出,这就起到“与门”的作用。

图6.7 逻辑“与门”
2.“或门”与多输入“或门”
如图6.8所示,当r1 或r2 中有一个脉冲输入就足以使神经元产生一个脉冲rc,这就是“或门”。
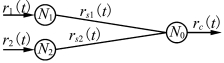
图6.8 逻辑“或门”(https://www.xing528.com)
3.“非门”
在神经系统中“非门”就是抑制性神经元。当神经元输入脉冲时,抑制性神经元会根据输入信号产生抑制性脉冲。抑制性神经元的输出波形虽然与兴奋性神经元的相似,但是它们的效果正好相反。
4.多输入“与或门”
在神经系统中还有一种如图6.9所示的特殊逻辑。有k 个输入,其中只要有n<k 个r(t)有脉冲输入就能使N0 产生一个脉冲。这就是多输入“与门”。r1 至rk 中,任意一个脉冲输入神经元就会有一个输出rc,这就是多输入“或门”。这两种规律被称为多输入“与或门”,这种逻辑门在信息处理中有它独特的用处。

图6.9 多输入“与或门”
以上种种逻辑关系在H-H 方程中是很容易表达的,只要调节连接强度、神经元参数,保证输入一定数量的脉冲后一个神经元能输出一个脉冲,就可以表示上述几个逻辑关系。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




