神经信息运算体系：声呐与感觉系统的信息处理机理研究

Ω 空间是一个距离空间，Ω 空间应该具有距离空间所有的特性。Ω 空间中的“元”不是一个数，而是一串脉冲序列，其中的运算规律与实空间有很大不同，具体分析如下。

1.Ω 空间的单元

实空间中的元是数，数字计算机中的元是一串二进制数（一串0、1 序列），Ω 空间中的元是一串神经脉冲序列。

假定神经脉冲的表示式为r（ta，Ti）。式中，ta 表示初始相位，Ti 是脉冲之间的时间间隔。对等周期脉冲序列，Ti 可改为常数T。脉冲序列中脉冲幅值和形状是一定的，所以脉冲波形不能代表任何信息，在这里可以忽略。与二进制数一样，序列的长短视比较的灵敏度需要而定。

神经脉冲序列通过神经元的变换规律可用图6．3所示的关系表示。其中，输入是一串脉冲序列ri，输出是另一串脉冲序列y。对于单输入、输出系统，输入脉冲序列一般不会与输出相同，输入和输出之间存在一定的映射关系，将其假定为f。由于前面已经证明过，输入与输出脉冲序列单调性是一致的，所以可以确定f 是单调递增映射。

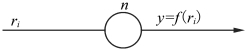
图6.3　神经元输入与输出之间的关系

假定兴奋性神经元的输出脉冲序列都为“正数”，相对地，抑制性神经元的输出则为“负数”。通常神经信息都是以兴奋性神经元输出作为信息，抑制性神经元的输出只是在运算中出现，不能作为独立的信息出现。这里所讨论的信息编码也就是指兴奋性神经元输出的脉冲序列。

2．两序列相加

实空间中存在确定的值，S 空间中的值只有相对大小，因此两个空间中的加法规律也有所不同。现做如下定义。

设有如图6．4所示的系统。假定有r1 和r2 两序列，相加后变为另一序列r3′

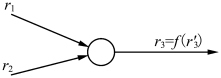
图6.4　一种可能的加法系统

式中，r′3 是两神经脉冲序列相加的当量脉冲序列，即用r′3 代替r1+r2 输入到神经元中，可使神经元输出保持不变。如果要让系统满足相加的关系，即要式（6-5）成立，则一定要满足下面两个关系。

①脉冲序列r1、r2 和r1+r2 具有如式（6-6）中的排序关系，频率曲线关系如图6．5所示。

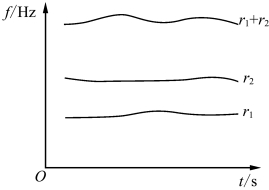
图6.5　r1、r2 和r1+r2 脉冲序列的频率曲线

②当r2 不变，r1 增加时，r′3 增加。同样，当r1 不变，r2 增加时，r′3 也增加。

只有满足上述①、②两个关系，才能承认脉冲序列存在加法关系。

对上述关系做计算机仿真是很简单的，只要在同一个H-H 方程中加入两脉冲序列r1 和r2 就可以计算了。最后用r′3 的排序规律可以证明加法规律。我们进行了部分仿真计算。以前的计算结果都是把输出脉冲序列变为符号序列，最后列表中都是一串串符号序列。这是因为两脉冲序列相加，相加后的“和”是r′3 而不是r3（见图6．4），但是我们尚无法得出r′3，所以无法按广义圆映射定义求出输出脉冲序列的确切符号。因此我们采用了另一种方法，也就是神经系统本身能实现的方法，通过比较等脉冲数的序列的时间长短来确定输出脉冲序列的大小，建立神经脉冲的排序规律。

当有两个输入信号输入到同一神经元时（见图6．4），两路信号输入存在关系

这里的r3=f （r′3 ）在实际情况下会比r1+r2 小，这是否说明式（6-7）的加法不成立？不是。在这里不能把图6．4中神经元的输出直接看作加法的结果，r3的大小变化仅仅能反映出①和②的关系是否存在。

加法系统的仿真示例：r2 输入脉冲为200Hz，波形如图5．15所示，峰值为Im=5μA；r1 输入脉冲频率为100～200Hz，Im=1μA。随着所加信号r1 的频率的提高，出现相应的脉冲输出时刻提前（见表6．1）。

表6．1　r2 不变，r1 频率变化与输出第16 个输出脉冲的时刻关系

注：由于这里一个细胞有两个输入，所以不能直接求出输出脉冲序列的符号序列，于是采用同样脉冲数下的输出所需时间作为输出指标，我们不必关心绝对时间长短，只要比较哪个时间长就行。

这里的r1 与r2 输入信号幅值不一样，是随意定的（幅值不一样也反映了神经元之间的耦合强度不同），这也反映更一般化的加法，输入幅值不一样确实会使输出频率产生变化，但是相对的输出时间长短次序还是保持不变。

在数字计算机上做加法运算实验就是在H-H 方程右边加上两串脉冲序列r1 和r2，但是还需注意避免两个脉冲正好叠加在一起使电流幅值超过H-H 方程所允许范围的情况。其实在神经元中不会碰到这一情况，因为神经元是由细胞的两个地方输入信号，而这里是把神经元当作集中参数来考虑的，所以就把两个信号在一个方程中直接加在一起。数值实验中出现这一情况时，可适当减小输入信号幅值，这样仿真的结果还是可认可的（这样做仅仅能证明可行性，因为集中参数和分布参数两者总有差别）。(www.xing528.com)

3．两序列相减

同样可以做神经脉冲序列相减的定义。还是借用图6．4作为讨论对象。设存在关系式

式中各元满足如下关系。

①当r1 不变，r2 增加时，r′3减少；当r2 不变，r1 增加时，r′3也增加。

②r′3不能为负，也就是说两序列相减不会出现负序列。

r2 是抑制性神经元输出，实现减法的回路还是与图6．4一样，只是其中一个信号是抑制性神经元发出的信号。把抑制性神经元的和兴奋性神经元的输出脉冲序列同时输入一个神经元，实际上是在做减法运算。

在做减法时要注意减法本身还有一个适应范围：r1 和r2 不能太接近（大小相近），因为两个信号太接近，会使r′3频率过低，若r′3频率低于ωc，会使神经元输出的“序”不呈单调关系。这样，输出就不能反映输入信号的变化。为避免这种情况，可改变连接强度（改变r1 和r2 的幅值）。一般需要做减法时总会多加上一个抑制性神经元，因此还是能够保证两者频率差距足够大。

这种减法限制太多，不太符合数学中定义的要求，但是从S 空间角度来看还是适用的。

4．神经信息运算网络

有了上述关系，则在Ω 空间内可以做进一步推算。设有如图6．6所示的神经回路，这是两层结构的神经网络。

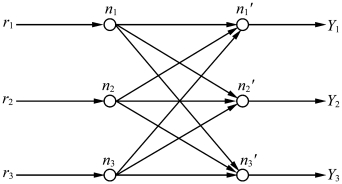
图6.6　一种神经信息运算网络模型（结构）

根据图6．6可得

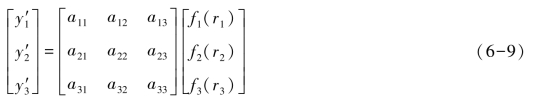
式中，aij是第一层第i 个神经元与第二层第j 个神经元的连接强度。y1，y2，y3是输出脉冲序列。f1，f2，f3 分别是第一层神经元输入输出之间的关系。

当f1，f2，f3 是单调递增函数时，按定理4．5，在S 空间中，可以把式（6-9）改为

这里的y′1、y′2、y′3是神经元n′1、n′2、n′3输入的当量脉冲序列，不是它们的输出。同样，由于神经元输入输出关系的单调递增特性，式（6-10）在S 空间中也可以改为

或写成向量形式

以上公式一般都不是等式，不符合实空间的矩阵定义，采用映射形式表达更好，因为这里的映射基本上可理解为函数关系，而且是单调递增函数，所以从S 空间的角度来看也可以考虑这一形式。但是要注意，这里的y1、y2、y3 不能在等式两边随意移动，因为这里的yi 只是表示与yi′保持相对应的序而已，或者说y1、y2、y3 不能与r1、r2、r3 进行比较和运算。

现代控制理论中的基本运算都是矩阵运算，利用矩阵能表达一切信号变换过程。式（6-11）成立，说明脑内至少能完成各种类似的运算，只是这是在S 空间中的运算。

5．神经系统运算小结

归纳上述分析，神经系统的基本运算单元是神经元。神经元的电生理过程可以分为两个阶段。

（1）分级电位阶段，分级电位只对输入脉冲信号进行累计。分级电位是进行运算的环节，主要实现加法，如有抑制性神经元输入则是减法运算，无法实现乘除运算。

（2）运算结果以动作电位形式表现出来，主要表现在动作电位在时间轴上的前后移动，神经元无法实现乘法运算，但可通过改变连接强度来弥补乘法的运算问题。

如果式（6-11）成立，则矩阵A 的特征值就可以决定系统的稳定性，这表明系统稳定性取决于神经元连接强度，取决于矩阵A。我们的目标是保持系统的不稳定性。

为什么能用一个神经元实现“多普勒效应”计算？为什么能用一个细胞实现相位计算？因为一个细胞能实现加减的运算（这里运算是在S 空间中），更重要的是在不稳定和不确定条件下实现运算。现有的人工神经网络中，一个神经元几乎什么也不能做。这些差异足以跳出现有的确定论的框框。