神经系统识别编码机理-理论神经信息学初探

神经系统能否识别“编码”？要使S 空间编码的假设真正成立，必须解决神经系统本身是如何识别这一编码的问题。如果能肯定“找不到神经系统识别S 空间编码的机理”，那S 空间理论肯定是有缺陷的，或其本身就是错误的。

在彻底解决这一问题之前，可先从两方面来考虑。首先，圆映射、符号动力学等理论能否反映神经系统的客观规律？只要所采用的理论方法遵循客观规律，则神经系统肯定能识别这种编码。“找不到神经系统识别该编码机理”只能是暂时的，随着研究工作的深入，以后一定能找到。其次，如果真的找不到，这就要考虑这种编码理论的正确性。

6.6.2.1　神经系统识别S 空间编码的基本原理

神经系统本身不可能知道什么是圆映射理论、符号动力学，更不知道距离定义。但这些并不重要，问题是神经系统能否按S 空间可排序规则判别脉冲序列的大小，或者说神经系统是否具有特定区分脉冲序列大小的方法，方法是否与符号动力学的区分方法相一致，而且区分的灵敏度是否一样高。

其实按S 空间脉冲序列排序规则（见第4 章），实质上就是按频率大小来排序。脉冲序列的频率f 可以用式（6-4）表示：

式中，n 是脉冲个数，t 是时间。

按式（6-4），要比较f 的大小有两种方法：一是保持时间t 不变，看n 的大小来衡量频率高低，这就是频率编码的方法；另一个是保持n 不变，看时间t 的长短，这就是S 空间的方法。再明确一次，比较两串脉冲序列大小只要看两串脉冲序列时间长短就可以了：时间短的就是频率较高，为大；时间长的频率较低，为小。这一规律应被严格证明才行。但由于证明过程太复杂，我们没有严格证明，但是我们用计算机在我们计算的范围之内实验过，判断方法都是符合这一规律的。为了便于理解，简要做些解释：两串脉冲序列的符号序列相同，表示两者的脉冲数相同，时间长短也相同。但是有一个小于一个周期的误差（见图5．2），这个误差有些大，但没有关系，只要再延长脉冲序列（增加n），这个误差会逐渐被放大，直到最后一位符号序列变了，就能看出脉冲序列大小。按距离公式，最后一位符号变化的位置越在后面，表示两串脉冲序列越接近，距离越小。(www.xing528.com)

6.6.2.2　识别时间长短的可能神经回路

由于神经系统还具有逻辑判别能力（见本章6．8 节），所以熟悉逻辑电路的人肯定能理解，比较两个脉冲序列的时间长短的神经网络是容易实现的。

如图6．2所示，判别脉冲序列长短的回路中，N1、N2 是兴奋性神经元，Q1、Q2、Q3 和Q4 都是抑制性神经元。回路的工作原理是：脉冲序列A 和B输入后，当脉冲A 和B 同时到达神经元N1 或N2 时，N1 还收到来自Q1 的信号，由于Q1 是抑制性神经元，所以它将使A 的信号减弱，因此N1 将没有脉冲输出。同样地，N2 也将没有脉冲输出。当A 的脉冲信号较早到达N1 时，此时没有抑制性信号输入，所以N1 就会输出一个脉冲。此后当脉冲B 到达N2 时，此时N2 已收到两个抑制性脉冲输入，因此N2 就不可能有脉冲输出。

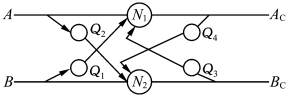
图6.2　判别脉冲序列长短的回路

这种比较回路只有在两个脉冲到达时间相差较大时才有效，但这并不影响分辨率。关键在于比较回路的输出在多少个脉冲数后出现这种时间差。如果几个脉冲后就有较大的时间差，说明两者相差很大；如果在几十个脉冲以后才出现较大时间差，说明两者相差很小。这一规律完全符合距离定义中的差别。

区别脉冲序列大小的回路可以找出很多，但是尚不清楚神经系统究竟采用的是哪一回路。神经回路还存在简并性，会有很多回路来判别脉冲序列的大小，各种回路结构都有可能在神经回路中存在。也许图6．2的示例不是生物神经系统中存在的，它仅仅是为说明神经网络是有可能判别神经脉冲序列大小的，即脑是能感知S 空间规律的。反过来，如果能找到神经系统识别脉冲序列大小的回路结构模型，也就能进一步增加S 空间编码理论作为真实神经编码的可能性。