两细胞间信息传递研究成果

突触是两个细胞连接的地方，如图5．13所示。突触由三部分组成：突触前（a2）、突触后（b2）和突触间隙（存在于a2 与b2 之间的间隙）。突触前是前一细胞（A）的轴突（a1）的末端，突触后是下一细胞（B）的树突（b1）的前端。

图5.13　神经元间的突触连接

每当突触前有脉冲到来，突触前在这一脉冲的刺激下就会释放一定量的神经递质，这种释放是按量子形式释放的。因为每一脉冲都是固定大小和固定形状的，所以突触释放的递质也是一定量的，每次脉冲到来，突触释放的神经递质量按下式计算［17］：突触前释放的神经递质量（突触强度大小）=量子释放数（m）×量子幅度（q）。

这些被释放的递质被突触后（b2）吸收后，会引起突触后离子通道的开放，离子通道的开放程度（在一定时间内）是不变的，在突触后膜形成的总的电流的波形也是一定的。关于这种电流波形的具体形态尚无文献报道，但由于这是可激发介质系统，波形将与离子通道的特性有关。图5．14是文献［18］给出的突触前和突触后电压的变化曲线。

有人把第一级细胞的输出电压信号Vc 乘上电导G 作为下一细胞（神经元）的电流输入值［19-20］，这在运算上常常是有效的。G 被看成下一细胞输入的“电导”。然而，这里其实根本不存在输入阻抗（电导）。要注意，这里的电压、电流的关系并不符合欧姆定律，因为这是可激发介质动力系统。但从S空间理论看，可以理解为下一细胞以Vc 作为输入电流波形（因为输入信号波形是可以任意变化的），而G 则是作为常数来处理，它可以反映细胞间的连接强度。因此这种输出电压信号乘上“电导”的方法还是可以被认可的。其实，在前面的计算中我们也是以脉冲序列作为输入信号的。

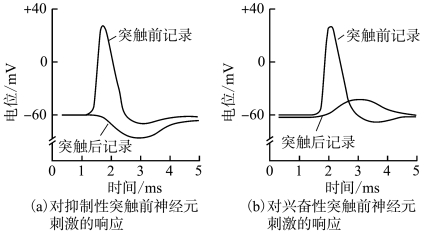
图5.14　抑制性和兴奋性两种细胞输出信号差异［18］

注意，前面的计算都是把脉冲序列作为电流输入信号的。按图5．14所示的电压变化曲线推算，突触后电流并不是矩形脉冲电流，文献［21］和［22］中涉及的电流波形也不是脉冲形式的。考虑到文献［21］和［22］中给出的电流波形，我们采用类似波形（见图5．15）来代替矩形脉冲，同样也可以得到与图5．3、图5．4相似的圆映射图形。这说明原有的符号动力学分析结果还是适用的，只是ωc 由原来的300Hz 降为30Hz 左右，反而更接近生物的实际状况。我们也可以从中看出，以图5．15的波形代替矩形脉冲也许可能更接近生理状态。(www.xing528.com)

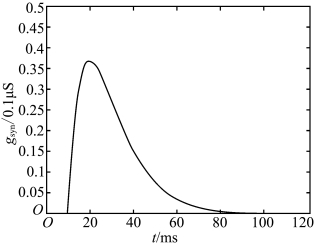
图5.15　神经元输入的电流波形

概括上述分析过程，前一细胞的一次兴奋，最后会引起下一细胞中注入一定的电流。我们尚不知晓注入电流的波形，但是每一次注入的波形应该是一样的。因此通过简化处理可直接把突触去掉，只要在前一细胞每次兴奋时，在对应时刻给后一细胞模型输入一定波形的电流即可。

由此，根据S 空间理论，无须考虑输入波形的具体形态，只要保证前一细胞每次脉冲信号产生时将一定波形的电流输入到下一个细胞（H-H 方程）就可以了。神经信号信息仅仅携带在神经脉冲之间的时间间隔上，所以第二级神经元输入的三角波或方波的周期变化必须与第一级神经元（H-H方程）的输出周期变化一致。这就实现了两个神经元串联时的信号传递过程。

当突触前有一脉冲信号时，突触后会产生一次电流注入，虽然假定注入电流波形保持不变，但要注意这只是在相当短的时间内的不变，这种不变可以持续几秒到几分。一般来说一串脉冲序列只有零点几秒，几秒时间已经足够了，不会影响信号处理。时间长了波形为什么会变？这反映在突触间的连接强度上，与突触的可塑性有关，也与其记忆有关。

不管是用矩形脉冲还是用图5．15所示的波形代替脉冲波形，如果经常有脉冲序列信号通过此突触，也会使突触后吸收更多递质，从而使输入的离子电流增加，这就是所谓的连接强度增加（这是可塑性的表现）。当连接强度变化时，图5．15所示的突触后电流波形也会产生变化，但这种波形变化仍然满足可排序性规律（参见第4 章）。

虽然神经元输出脉冲波形与输入波形无关，但是我们用图5．15的波形代替矩形脉冲后，如前所述，神经元的ωc 将大大降低，由原来的300Hz 降到30～100Hz（视输入信号的幅值不同而变），这表明我们还是需要适当考虑输入波形。输入波形究竟应该是怎样的？虽然我们还没有找到对此进行说明的确切可信的文献，但这并不影响我们的分析过程。