广义圆映射的概念及其重要特性分析

在正常神经生理状态下，神经元的输入往往不是等周期脉冲序列，因此上述圆映射规则还不能直接使用。为此，文献［4］提出了广义圆映射的概念。广义圆映射只是把圆映射再拓广一点。圆映射的输入信号是等周期信号，而广义圆映射的输入信号可以是非等周期的。

在图5．2（a）中，ri 表示输入信号，δi 表示输出信号，可求出θi 与θi+1的关系，这是原来的圆映射。为了适应神经元的实际工作情况，把输入信号的脉冲周期τ 从固定的变成随时间变化的τ1，τ2，…，τn［见图5．2（b）］。虽然其他所有的处理方法都一样，包括符号动力学分析方法都是一样的，但是，此时已不能画出像图5．3那样的很有规则的函数图形。

广义圆映射还具备如下一个重要特性。

【定理5．1】如果有三串脉冲序列是可排序的脉冲序列，分别将它们输入H-H 方程，输出也是脉冲序列。若将它们按广义圆映射方法进行符号化，所得三串符号序列是可排序的。

采用计算机仿真验证，将图5．11所示的频率曲线（正弦曲线的一部分）所对应的脉冲序列输入到式（5-1），可以得到如表5．4所示的脉冲序列，对输出的脉冲序列运用广义圆映射方法，取得如表5．2所示的符号序列。

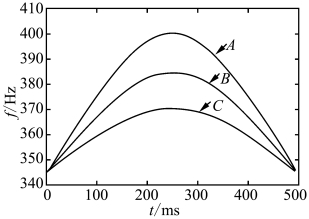
图5．11　三条可排序的脉冲序列的频率曲线

表5．4　图5．11中对应的脉冲序列与输出的符号序列的排序关系(www.xing528.com)

如图5．11所示，图中三条脉冲序列的频率变化曲线起始点相同，频率幅度不同，同一时刻按频率从大到小排列是fA＞fB＞fC，相应的神经元输出脉冲序列的符号序列列于表5．4。对表中的符号序列进行排序后可知，A，B，C 三条曲线各自对应的符号序列SA，SB，SC 的大小顺序是SA＞SB＞SC。高幅值的频率变化曲线对应的符号序列大，而低幅值的频率变化曲线对应的符号序列小。

表5．2中不同频率的脉冲序列的排序也可以用广义圆映射来解释。不同频率的等周期脉冲输入，相当于将图5．11中几条频率曲线变为不同高度的水平线。不同高度的水平线，还是满足排序定义。这表明标准的圆映射是广义圆映射的一个特例。

与定理5．1 对应，存在如下逆定理。

【定理5．2】设有两个可排序脉冲序列A 与B，分别输入到同一神经元，其相应的输出脉冲序列的符号序列分别为SA 和SB。如果有关系式SA＞SB，则脉冲序列A＞B。

用反证法很快能证明这一点。