首先,考虑一个神经元在恒定频率的脉冲电流刺激下的响应,神经元用式(5-1)所示H-H 方程来描述,以神经元的轴突上的电位变化作为输出[9]。
方程中的相关参数值如表5.1所示。
表5.1 H-H 方程所用参数

顺便提一下,这些是H-H 方程作为局部细胞膜电位与离子通道电流的关系时的参数。与现在大部分文献一样,我们直接将H-H 方程当作整个细胞的输入输出关系,这样,反映单位面积的量“cm-2”都可以去掉。以后我们在方程中表示某些输入信号时,写出的量常去掉“cm-2”。
当输入为等周期脉冲序列时,输出是一串脉冲序列,而且输出脉冲序列中每一脉冲的幅值和波形形态是相同的,这反映了可激发介质动力系统的特性。可激发介质动力系统还具有另一个性质:无论输入脉冲信号的波形形态是矩形还是三角形,输出的脉冲信号波形都是一样的。真正反映输入信号变化的只是输出脉冲序列中脉冲之间的时间间隔。利用H-H 方程仿真计算得到的结果是一串很不规则的脉冲序列。要分析这串脉冲序列中的时间信号,圆映射可以发挥作用。具体处理方法可按图5.2(a)进行,由δi 得出θi。其中ri(i=1,2,…,n)为神经元输入信号(刺激),在这里作为圆映射的时间刻度,τ 为输入脉冲之间的时间间隔,δi 为神经元的输出信号,相位差θi 为神经元第i 个输出脉冲与最邻近的输入脉冲间的时间差。
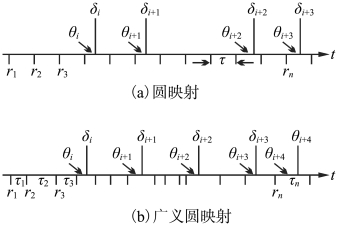
图5.2 圆映射(https://www.xing528.com)
这样一串输出脉冲序列按图5.2(a)的规律可得一串相位序列
![]()
式(5-6)是由式(5-1)得出的,理论上根据式(5-1)可求出θn 与θn+1之间的变换函数,但实际上求解很困难。根据θn 与θn+1数据可画出函数关系图(见图5.3),从图5.3可以看出θn 与θn+1 存在着非常有规律的函数关系,这就是圆映射图(图中取相对坐标θi=θ′i/τ,其中τ 为输入信号周期,为图5.3中实际的时间间隔)。
根据圆映射理论分析,图5.3是一个非常好的单调递增映射,这一规律为了解神经编码打下了坚实的基础。接下来只需按照圆映射规则来分析这一脉冲序列。
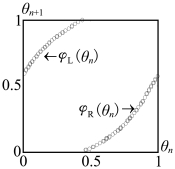
图5.3 输入脉冲周期为2.6ms 时,神经元输出的圆映射图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




