若在S 空间中进行信息处理,则信息科学中很多现有的定义都要有所改变。
【定义4.7】相同波形(零阶序相同的波形)
把波形的峰谷点取出,这些峰谷点就是波形的单调性转折点。如果这些转折点的排序相同,则波形相同。如图4.3所示两条曲线,按峰谷点排序,都是a-c-e-f-d-b 的次序,所以定义这两条曲线为零阶序相同的波形(或称:从零阶序角度看,两条曲线是相同的)。根据这一特点,不同频率、不同幅值的正弦波在S 空间中是零阶序相同的波形。
【定义4.8】Δ 同序点
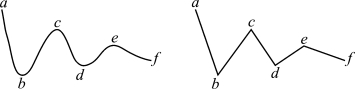
图4.3 零阶序相同的波形
由于人们习惯了实空间,故从实空间变为S 空间时存在着具体的处理问题。如图4.4(a)所示,a,b 两点在同一高度,所以它们在峰谷点排序中处在同一序上,被称为同序点。图4.4(b)所示的a,b 两点,在实空间中实际上是有差别的,即a-b=ε。但当ε 小于某一阈值Δ(0<Δ)时,可以认为ε=0,a,b 两点可以被称为同序点。这种情况在实际系统内是经常遇到的。从理论上来说,要比较两者大小,需要靠无限长的轨道来衡量,但是真正的神经系统是靠有限长的轨道来衡量的。所以一定存在Δ>0,当两者之差小于Δ时,a,b 两点就被认为是Δ 同序的点。如图4.4(b)所示,当a,b 两点之间相差很小时,a,b 可称为Δ 同序点。
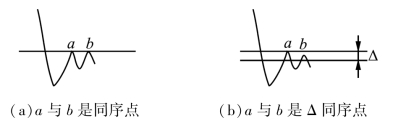
图4.4 同序点
【定义4.9】滤波
在S 空间中也有滤波的概念。从图4.5可看出,由a 曲线变为b 曲线就是一个滤波过程,要找准相对应的点,才能去掉高频波分量。(https://www.xing528.com)
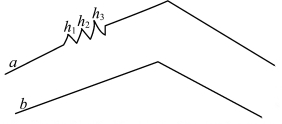
图4.5 滤波
【定义4.10】n∶m 相关
与相同波形相比,两曲线中可能出现有几个点不同序的情况。如图4.6所示,两曲线各有8 个峰谷点。若去掉e 点,则两曲线的对应峰谷点(7 个点)排序完全一致。此时称两曲线是7∶8 相关的。

图4.6 7∶8 相关的两曲线
【定义4.11】选择性相关
在寻找两条曲线对应的峰谷点时,可以去掉一些峰谷点,这就是两条曲线的选择性相关。选择的对应点不同,相关的效果也不一样。从图4.7可以看出,第一条波形曲线与第二条波形曲线相比较,如只考虑a、b、c、d 四点(为便于讨论,这里只取峰点,不考虑谷点,这不影响讨论分析),两者对应点的排序是相同的。如果去掉a、b、c、d 四点,则第一条曲线与第三条曲线对应点的排序相同。这里已经使用了相关和滤波运算。
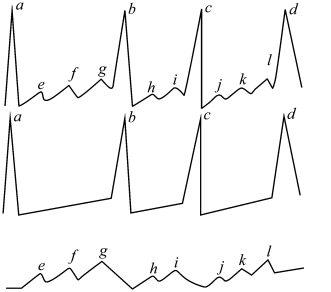
图4.7 不同对应点进行相关和滤波运算
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




