OGY 方法,是由Ott、Grebogi 与Yorke 三人提出的[14],它是混沌控制研究中影响最大、最早的方法。OGY 方法提出后,混沌控制的研究才全面开展起来。
OGY 方法的思想实质是:在无穷多不稳定周期轨道稠密地分布于混沌吸引子闭包中,采用短时微小扰动方法使混沌态变为稳定的周期运动。下面简要地介绍OGY 方法的控制过程。
假设有一方程
![]()
式中,x 是D 维向量,ρ 是可调节的系统参数(或称控制量)。这是一个适合描述任意动力系统的一般性方程。
如果描述系统的动力学方程未知,系统完全由测量得到的数据来观察。如果系统在t 时刻的状态是Y(t)∈D,那么所测得的时间序列的标量函数为Z(t)=Z(Y(t))。这样我们可以构成嵌入维向量,并通过庞加莱映射,给出截面上的点列,并可得出前后两点之间的映射关系:(https://www.xing528.com)
![]()
为便于说明问题,假设系统(2-101)是一简单二维系统(见图2.72)。假设这一系统具有一个不稳定的不动点ξ0(ρ=ρ0),经过该点有一个稳定流形s和一个不稳定流形u。假定轨道经过一段时间后来到ξ0 附近的ξn 处,点ξn的运动轨迹是不断向不稳定流形靠近的,同时又沿着不稳定流形无限扩展[见图2.72(a)]。此时我们就变动系统可控参数ρ→(ρ+Δρ)=ρ1,使得ξ0 移动到ξ′0[见图2.72(b)],此时ξn 按图2.72(b)中所示方向运动,使轨道向稳定流形s 靠拢。我们总可以多次调整ρ1 大小,使ξn 变为ξn+1点,此时使ρ1 恢复到ρ,ξn+1点就落在稳定流形附近运动,然后系统状态ξn+1会自动向不动点ξ0 方向运动[见图2.72(c)]。当系统接近ξ0 后,又会沿着不稳定流形再一次离开不动点。由于系统是非线性的,轨道不会趋向无穷远,总在一个有限空间内无穷弯曲,经过一段时间轨道又回到ξn 附近,然后再重复上述过程,使系统永远处在周期运动状态。取不同的ξn 和领域,可以得到不同的周期运动。从而达到控制混沌轨道的目的(具体算法和控制可见文献[14]至[16])。
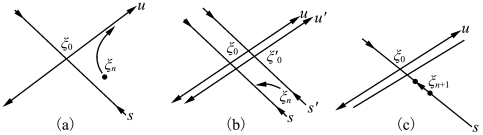
图2.72 OGY 方法混沌控制过程
OGY 方法算是最早提出的混沌控制方法之一,也是最典型的控制方法。自此之后就兴起了混沌控制研究的热潮。还有很多控制方法可参考有关资料[16]。混沌同步也可理解为对混沌的一种控制方式。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




