【摘要】：圆映射理论主要用来讨论两系统同步和同步分岔等问题，应该放在同步这一节上。在这里提出圆映射，主要也是希望读者不要以为圆映射仅仅是为了解决同步问题。为表示差别，称式为圆映射提升，称式为圆映射。想要进一步了解圆映射，请见文献［6］和［11］。神经元在等周期脉冲序列的输入下，其输出的圆映射如图2．70所示，这是单调提升圆映射，后面还会进一步讨论。图2.70具有等周期作用的神经元模型圆映射图
圆映射理论主要用来讨论两系统同步和同步分岔等问题，应该放在同步这一节上。在本书中，圆映射并不用于同步问题，它主要用来分析神经元脉冲序列的问题。圆映射和符号动力学一起将解决神经脉冲序列的排序问题，这是本书所依据的最根本的理论基础。在这里提出圆映射，主要也是希望读者不要以为圆映射仅仅是为了解决同步问题。
有满足关系式
的实函数f（x）所表示的映射
如果把f（x）写作
则g（x）是x 的周期函数：g（x+p）=g（x）。由于g（x）是周期函数（在这里假定周期为1），则相差整数的x 可以看作等价。式（2-81）可写成
(www.xing528.com)
从这个意义上，T 是圆到圆的映射，S1→S1，简称圆映射。它也是庞加莱映射之一［6］。
式（2-82）与式（2-84）虽然是等价的，但是式（2-82）是实轴上的映射，式（2-84）是圆上的映射。为表示差别，称式（2-82）为圆映射提升，称式（2-84）为圆映射。式（2-81）还可进一步推广为
式中，N 是整数，称为相应的圆映射（2-82）或式（2-84）的拓扑度。N=0 相当于一种区间映射。
的映射总有大于0 的拓扑熵，N=-1 的光滑映射总是通过倍周期分岔到达混沌。想要进一步了解圆映射，请见文献［6］和［11］。
神经元在等周期脉冲序列的输入下，其输出的圆映射如图2．70所示，这是单调提升圆映射，后面还会进一步讨论。
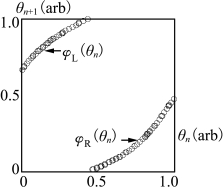
图2.70 具有等周期作用的神经元模型（H-H 模型）圆映射图（周期为2.6ms）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
