混沌特性探讨：生物声呐与感觉系统信息处理机理

1．分岔图的普适常数

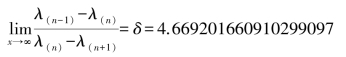
很有意思的是，任何单峰映射都具有这样的常数，这说明许许多多的非线性函数具有共同的特性。这个数被称为费根鲍姆数（Feigenbaum number）。这是十分有意义的事，可惜人们还不太理解它。

2．自相似性

在分岔图2．36的混沌区中有很多窗口，这些窗口内表现出非混沌态。

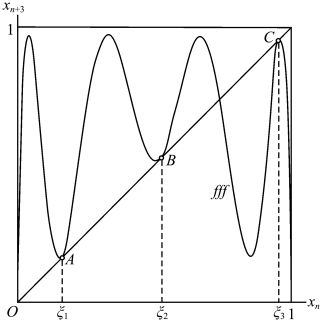
以周期3 窗口为例进行分析（见图2．39），周期3 窗口的成因可以从图2．40看出，当λ 再增加时系统就进入周期3 窗口，函数曲线与45°线在A、B、C 三点相切，这时就是图2．39窗口中的ξ1、ξ2、ξ3 三点。以后随λ 的增加，函数曲线与45°线相交就表现出窗内口的复杂过程。对比图2．36，可看出两者相似过程。而在窗口3 的混沌区中又会有各种窗口，如果再把这些窗口放大，又可看到与周期3 类似的图形，而且这个过程又会在新的窗口再现，构成一种不断嵌套的形式。这种现象几乎在所有的迭代系统中都存在。这是十分有趣的现象（后面还会再讨论）。

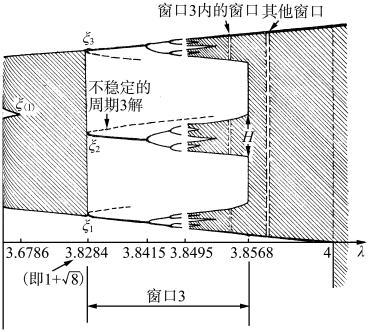
图2.39　周期3 窗口

(www.xing528.com)

图2.40　周期3 的成因

3．阵发混沌

当λ 较小时就进入阵发状运动——阵发混沌。当图2．41中迭代曲线在A、B 和C 处还没有与45°线相切但很接近时，迭代轨道会在这三点处的狭小通道中（见图2．41）“停留”很长时间。当轨道远离这三点，就会像图2．36那样处于混沌态。而一旦落于图2．41所示的狭小通道中，会像处在近似稳定态，这样在时域上就像图2．42那样呈阵发混沌。

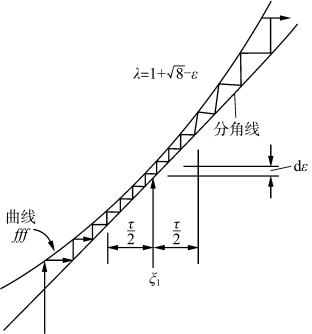
图2.41　阵发混沌的成因

图2.42　阵发混沌