【摘要】:我们可以分别求出当F、J 两点在45°线上时μ 与λ 的关系式Arnold 舌头如图2.32所示。图2.32Arnold 舌头F 和J 是两临界点,F 与J 之间的点都是稳定状态。图2.33多个Arnold 舌头μ 是输入信号的幅值,反映系统与耦联信号(输入)的连接强度。这样我们可以把图2.33与文献上典型的Arnold 舌头[6]联系起来。图2.34Arnold 舌头与参数关系
在图2.31中能形成周期解的是折线(以两倍周期为例),在改变参数μ、λ 的值时,EJIHF 会与45°对角线相交,交点可能有多个,但是这些交点的稳定性与线段斜率有关,与IJ、FH 等线段相交,则是不稳定的交点,与HI、JF线段相交才是稳定交点。与JF 相交的点有很多(从J 点一直到F 点),都是稳定交点。这些交点的位置取决于μ 和λ。其中J 和F 是两个极限的点。我们可以分别求出当F、J 两点在45°线上时μ 与λ 的关系式

Arnold 舌头如图2.32所示。式(2-56)和(2-57)分别对应图2.32中的曲线C1 和C2。

图2.32 Arnold 舌头
F 和J 是两临界点,F 与J 之间的点都是稳定状态。图2.32中灰色区域,就是稳定的参数区。
如图2.32所示的Arnold 舌头是由于线段FH 所形成的舌头,斜率与FJ相似的线段有很多,用同样方法可以找出其他多组像C1 和C2 的曲线,可以求出很多舌头(见图2.33)。(https://www.xing528.com)
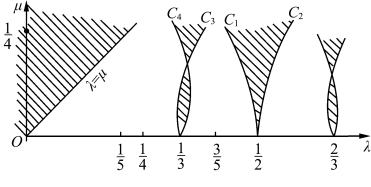
图2.33 多个Arnold 舌头
μ 是输入信号的幅值,反映系统与耦联信号(输入)的连接强度。λ 反映输入信号频率与系统本征频率之比(或周期之比)。这样我们可以把图2.33与文献上典型的Arnold 舌头[6](见图2.34)联系起来。

图2.34 Arnold 舌头与参数关系
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




