在同步中,总涉及两个频率,如ω 和ω′。同步以后,共同频率Ω 是什么?是ω 还是ω′?还是取ω 与ω′的中间值?
在接收电台信号的电路中,电路的频率一般都会跟着外来信号频率“走”,也就是Ω=ω外(外力)。两只完全相同的挂钟(但固有振动频率略有差异)通过木墙的耦合作用而同步时,其频率Ω 应该介于两者之间,而不会是一个俘获另一个。两个风琴管的同步也应如此。
为了更清晰地了解同步过程,下面来具体分析一个同步系统。假设有一个水箱,用弹簧把它悬挂起来(见图2.27)。水箱底部有一小孔,从小孔中有水滴滴出。开始时由于水的表面张力,水滴不会滴下,当水滴渐渐变大后,水滴重力超过表面张力,水滴就会滴下。然后由于小孔不断流出水,又会形成小水滴,水滴渐渐长大,再滴下,这种规程会周而复始地进行,形成一周期运动。当水箱不动并保持水箱的水面在同一水平面高度时,水滴的质量随时间变化过程呈等周期锯齿形曲线,如图2.27(a)所示。S0 是最大表面张力下水滴最大值,滴下时每次水滴都一样大。当水箱以一定频率做上下运动时,水滴大小就会产生变化。假定它是按图2.27(b)所示的规律变化,这时,锯齿波的周期就会产生变化。现在来仔细分析这一周期变化过程。
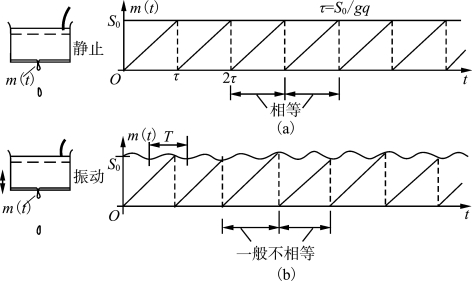
图2.27 同步的例子
按图2.28取无因次量纲,可以求出关系式
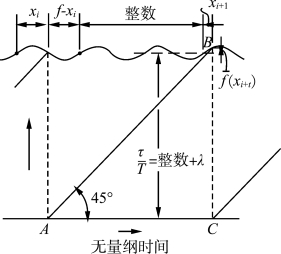
图2.28 圆映射分析
![]()
式中,τ/T=整数+λ,这里的λ 是τ/T 非整数部分,也可用{τ/T}表示。
按式(2-55)可解出xi+1=φ(xi)。(https://www.xing528.com)
为了计算方便,把输入信号改成三角波。其参数如图2.29所示。
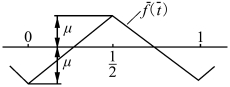
图2.29 三角波输入信号
φ(xi)的函数曲线如图2.30所示。
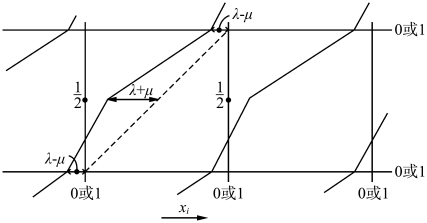
图2.30 φ(xi)的函数曲线
如果把几次迭代放在一个图上,就可得图2.31。
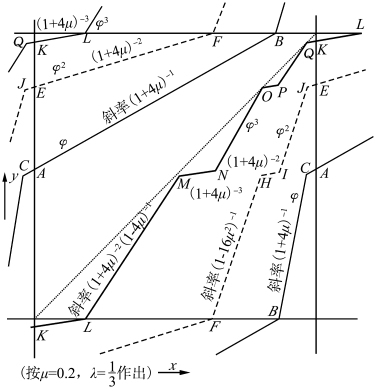
图2.31 多倍周期映射
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




