自然界中能产生自发振荡的系统及其特征

在自然界中稳定的周期运动是如何产生的？用什么样的数学可以描述这种机理？周期运动有如下几种可能。

（1）受迫振动

对系统输入周期信号，这样可以保证有周期信号输出。

如把P（t）=Asin（ωt）输入到系统中去，用它来保证系统输出稳定的周期信号，这就产生了“第一推动力问题”。P（t）=Asin（ωt）是从哪里来的呢？在自然界中有否没有外力能够自动产生振荡的系统？

（2）具有中心点的系统

是中心流形系统，它能产生周期运动，但它不能产生稳定的周期运动。这种与外界没有能量交换的系统称为保守系统。(www.xing528.com)

（3）振荡方程

由控制理论或动力系统理论可知：假定x 代表位移，则x 的两阶导数代表加速度，乘上质量m=1，这就是第一项，相当于惯性力；第二项是与速度有关的项，g（x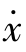，）相当于阻尼力；第三项是恢复力f（x）=V（x）。其中V（x）是势函数。f（x）是x 的函数，表示与位置有关的力，我们称其为恢复力。它与V（x）的导数有关，因此可以把V（x）理解为与势能有关的函数，所以称它为势函数。方程的最后一项则是与时间有关的外力p（t）。

要使系统自动产生振荡，系统必须是自治的，即p（t）=0，它是保守系统。由于存在阻尼项，所以运动是衰减的。因此，保守系统不可能出现稳定振荡。要保持稳定振荡，就必须有外加能量加入。如果阻尼是负的，则二阶特征方程的根实部为正，就会出现不稳定的焦点和节点。负阻尼系统表示有能量加入。系统轨道将趋向无穷大，还是不能实现稳定周期振荡。

上面三种情况虽然都能产生振荡，但都不能自发地产生稳定的振荡。