【摘要】:前面讲的很多分岔都是静分岔,主要集中于平衡点多少的变化。还有一种分岔会使系统的动态行为产生变化,我们称之为动分岔。Hopf 分岔就是动分岔的一种。图2.18Hopf 分岔尺子与轴的夹角是极坐标的角度φ,设尺子均匀转动,即把式和式改为直角坐标形式,得到当λ<0 时,系统稳定在不动点(0,0);当λ>0 时,系统稳定在常态,φ=ω,即当时间趋向无穷大时,系统趋向一个稳定的周期轨道,这一轨道称为极限环[见图2.18]。
前面讲的很多分岔都是静分岔,主要集中于平衡点多少的变化。还有一种分岔会使系统的动态行为产生变化,我们称之为动分岔。Hopf 分岔就是动分岔的一种。
设一单变量ρ 系统

它有一个参量λ。容易看出,当λ<0 时,系统有一个稳定平衡点ρ=0;当λ>0时,有两个稳定平衡点![]()
现在设想ρ 是极坐标中距离,即设(x,y)平面上有一可绕原点O 转动的尺子,沿着尺子轨道上有一小球(x,y),小球与原点之间有一条橡皮筋拉着[见图2.18(a)]。当尺子以一定的角速度ω 运动时,小球由于离心力作用,会沿着尺子向离开原点方向运动。由于小球又受橡皮筋的弹性力影响,最后只能平衡在两力相等处。小球运动轨迹就是图2.18(c)中粗黑线画的圆。
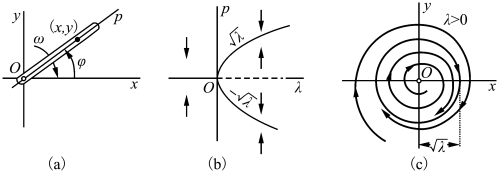
图2.18 Hopf 分岔(https://www.xing528.com)
尺子与轴的夹角是极坐标的角度φ,设尺子均匀转动,即
![]()
把式(2-36)和式(2-37)改为直角坐标形式,得到![]()

当λ<0 时,系统稳定在不动点(0,0);当λ>0 时,系统稳定在常态,φ=ω,即当时间趋向无穷大时,系统趋向一个稳定的周期轨道,这一轨道称为极限环(limit cycle)[见图2.18(c)]。系统(2.37)的极限环方程是x2+y2=λ。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




