单参数一维系统分岔的分类

分岔现象有很多形式，上面是单参数一维系统的一种分岔，此外还有很多分岔形式。

1．鞍结分岔（saddle-node bifurcation）

设有一系统如下：

相应的势函数为V（x，λ）=。鞍结分岔与相应势函数如图2．8所示。

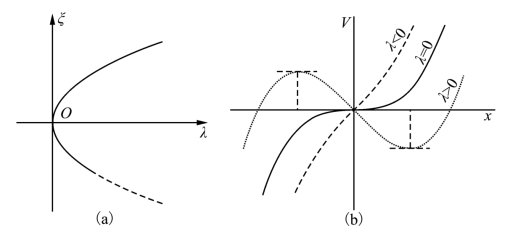
图2.8　鞍结分岔与相应势函数

λ=0 是鞍结分岔点。鞍结分岔在突变论中称折叠（fold）突变。

2．跨临界分岔（transcritical bifurcation）

设系统如下：

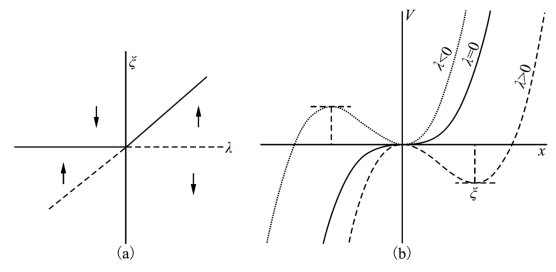
相应的势函数为V（x，λ）=。跨临界分岔与相应势函数如图2．9所示。

3．叉式分岔（pitchfork bifurcation）

(www.xing528.com)

图2.9　跨临界分岔与相应势函数

设系统如下：

相应的势函数为V（x，λ）=。叉式分岔与相应势函数如图2．10所示。

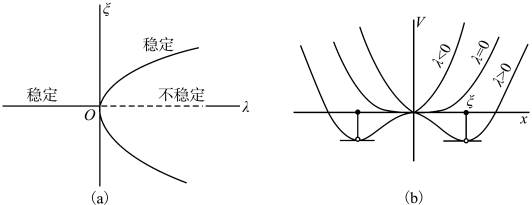
图2.10　叉式分岔与相应势函数

有些系统分岔点会随某些参数变化而变化，如系统

它的分岔见图2．11（a），图中A 与B 两点都是鞍结分岔点。相应的势函数为V（x，λ）=-λx，V（x，λ）随λ 变化如图2．11（b）所示。

如果把λ 当作输入信号，在势函数线上有一小球，则小球总是随势函数线的变化趋向最低平衡点，以小球的运动作为系统输出，在这里适当加上噪声作用于小球，则噪声可以帮助小球跨越阈值，这也就是随机共振的一个基本思想。

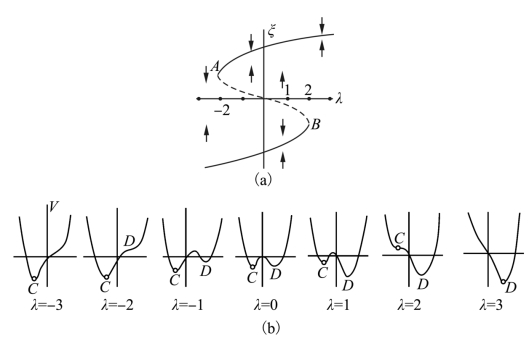
图2.11　参数λ 变化使势函数产生变化