生物声呐感觉系统信息处理机理研究：一个分岔例子

分岔是非线性所特有的现象。为了建立分岔概念，先来研究一个例子。

假定有一倒摆如图2.3所示。倒摆的下端用螺旋弹簧支撑着，弹簧刚度为2ka2。当偏角x=0 时，弹簧处在未变形状态（即平衡状态）。摆杆长l，不计质量，球的质量为m，不考虑阻尼，摆的运动方程是

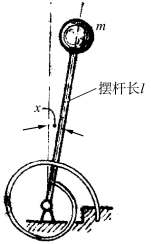
图2.3　倒摆

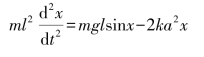
当x＜＜1 时，我们用来代替sinx，于是得

注意，不能用x 代替sinx，因为这样得到的是一种线性化的模型。用线性化的模型可以说明x=0 这一平衡位置是否稳定，但会丢掉非线性现象——分岔。因为分岔是非线性系统特有的现象，要研究分岔，必须采用非线性模型。在式（2-17）中，含x3 的那一项体现了系统的非线性。

系统的平衡点由方程（2-17）右端为零求出。当mgl≤2ka2 时（相当于质量较轻，而弹簧刚度较强），系统有一个平衡点x=0；当mgl＞2ka2 时（球的质量较重，而弹簧刚度较弱），系统将有三个平衡点，它们分别是x=0 和x=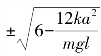（注意，这里仍然假设x＜＜1）。

平衡点的稳定性，由x 在平衡位置的二阶导数的正负号确定。如果为正，平衡位置不稳定；为负则稳定。其导数是

在x=0 处，x 的二阶导数有一项为mgl-2ka2。当mgl＜2ka2 时，x=0 是稳定的；当mgl＞2ka2 时，则是不稳定的。临界状态是mgl=2ka2，还有两个平衡位置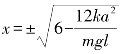，此处导数的值等于-2（mgl-2ka2），因mgl＞2ka2，所以这两个平衡位置都是稳定的。

我们把平衡点的x 值写成ζ。设系统的物理量a，l，k 等都是常量，m 是所谓控制参量（control parameter）。让m 由小变大，于是ζ 与m 之间的关系如图2．4（a）所示。

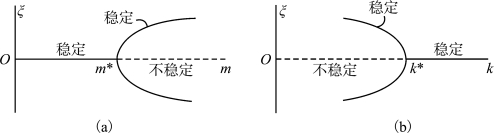
图2.4　m 和k 分别作为控制参量时的分岔图

图2．4（a）中m*=为临界点。当m（它不是时间的函数）由小于m*跨越到大于m*时，ζ 的值将发生分岔。在x=0 处，当m＞m*时不稳定，真正稳定平衡位置将分为两点，在图2．4（a）中由上支或下支给出。m=m*这一点就是参数空间（parameter space，这里就是m 轴）中的一个分岔点。由分岔点构成的集合称为分岔集（bifurcation set），在这里分岔集就是一个孤立的点。(www.xing528.com)

把哪个量当作控制参量是可根据需要和可能而定的。假如这里采用弹簧刚度作为控制参量，而令m 和其余的量一样不变，则相应的分岔图将如图2．4（b）所示，其中是k 的分岔值，分岔集由k=k*这一孤立的点组成。

若在式（2-17）中去掉立方项，那么ζ 与m 的关系或者ζ 与k 的关系将由图2．4（a）、（b）分别变为图2.5（a）、（b）。

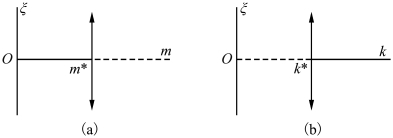
图2.5　线性化系统的分岔图

当m=m*（或k=k*）时，系统将处于“随遇平衡”；而当m＞m*（或k＜k*）时仍只有一个平衡态。其实图2．5可看作图2．4在｜ζ ｜极小时把曲线近似为直线而得到的一小部分图形。前面已经讲过，线性化理论只是一种局部的（local）理论，线性理论没有分岔这一现象。

分岔值m*，k*也就是常说的临界值（critical value）。

如果在式（2-17）中引进无量纲化时间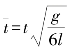，则式（2-17）可改写为

式中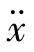，代表，参量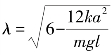。于是式（2-19）同样代表了图2．3的倒摆系统，其实有些地震仪器本身的简化模型就如图2．3所示。

式（2-19）所受的回复力是

即式（2-19）是非线性系统

的一个特例。式中λ 是参量。今后为方便起见，f 对x 的导数用f′（x，λ）表示，而不用

对于式（2-20），λ=0 是临界值或分岔点，参量空间中的分岔集就是这一点本身，这是一个折叠型突变，如图2．6所示。