考虑一般的二维自治系统
求奇点的位置只要令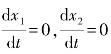
，也即
同时满足式（2-10）两方程的解就是由这两方程所确定的曲线之间的交点。对于线性系统来讲，方程（2-10）所确定的都是直线，所以只有一个交点。也即，对于线性系统来讲只有一个奇点，所有线性系统在没有外力的情况下平衡点一定在原点（0，0）（见图2．1），它具有全局性质。而对于非线性系统，由这两方程确定的是两条曲线，所以其交点可能不止一个，可以有多个。也就是说，非线性系统可以有多个平衡点。这一点是很重要的，如果一个生态系统满足线性方程，则在这一生态系统中，所有物种最终都将毁灭（回到原点），只有非线性才能使生态系统存在（离开原点）。
要了解非线性系统中各奇点的性质，可采用在奇点附近范围内局部线性化的方法。
例如：求下列系统所描述的相平面图。
该系统的奇点是x=0，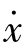
=0 和x=-2，
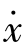=0。这两个奇点的性质可由下述分析得知。先在原点处附近对方程（2-11）线性化，得
它的特征方程为
两个根为
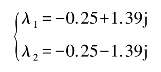
因此这个奇点是稳定焦点。(www.xing528.com)
在奇点（0，-2）附近，可对方程（2-11）做如下改写。
令
y=x+2
可得
在y=0，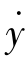
=0 附近线性化，得
特征方程为
上式的两个根为μ1=1．19，μ2=-1．96。
因此奇点（-2，0）为鞍点。知道了这两个奇点性质，我们就可以画出非线性方程（2-11）的相平面图（见图2.2）。
方程（2-11）所示系统的初始状态如果处在图2.2的阴影线范围内，系统最终都会趋向原点稳定下来，阴影线范围内称为局部稳定区；如果初始状态落在其他区域，则都会趋向无穷远处。非线性系统一般不存在全局的性质，在这里原点是局部稳定点，不是全局稳定点。
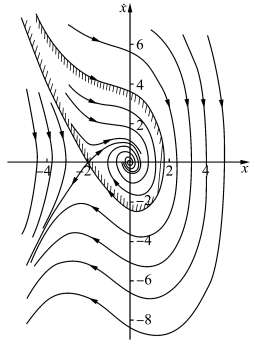
图2.2 方程（2-11）的相平面图
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
