【摘要】：假设在原点处方程（2-1）中的f1和f2是解析的，并假定原点是奇点，则f1（0，0）=0 和f2（0，0）=0。令a11=a1，a12=b1，a21=a2，a22=b2，则方程（2-4）可近似为式（2-5）是常系数齐次线性系统的一般形式，它可改写成二阶微分方程式中，x=x1，。其他奇点可由图2．1分别表示。对于没有外力作用的线性系统，奇点位置一定在原点处。奇点又称平衡点，也可称为不动点。奇点的性质决定了系统全局的性状。
假设在原点处方程（2-1）中的f1（x1，x2）和f2（x1，x2）是解析的，并假定原点是奇点（奇点不在原点处也可以通过坐标平移把奇点移到原点），则f1（0，0）=0 和f2（0，0）=0。
将f1（x1，x2）和f2（x1，x2）在原点（0，0）处展开成泰勒级数，得
式中，gi（x1，x2）（i=1，2）为三次方或更高次方项。
在原点附近，x2i（i=1，2）很小，后面的高次项将更小，这样在式（2-4）中线性项占主导地位。令a11=a1，a12=b1，a21=a2，a22=b2，则方程（2-4）可近似为
式（2-5）是常系数齐次线性系统的一般形式，它可改写成二阶微分方程
(www.xing528.com)
式中，x=x1，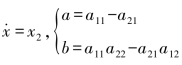
。方程（2-6）的解的性质取决于它的特征方程
的根。
假设式（2-7）的两个根分别是λ1 和λ2
图2．1给出了不同根的位置和相应的原点（0，0）附近的相图。
当特征方程具有两个负实部的复数根时，相图中有稳定焦点；当有一正一负两个实部根时，相图中具有鞍点。其他奇点可由图2．1分别表示。对于没有外力作用的线性系统，奇点位置一定在原点处。奇点又称平衡点，也可称为不动点。奇点的性质决定了系统全局的性状。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
