太赫兹波生物水分含量检测原理与误差分析

由于太赫兹波的波长范围是30μm~3 mm,波长大于可见光与红外波,因此太赫兹辐射通过新鲜的生物组织切片时不容易发生散射,在此我们假定散射效果可以忽略。根据Lambert-Beer定律可知,光通过物质后的透射率遵循：

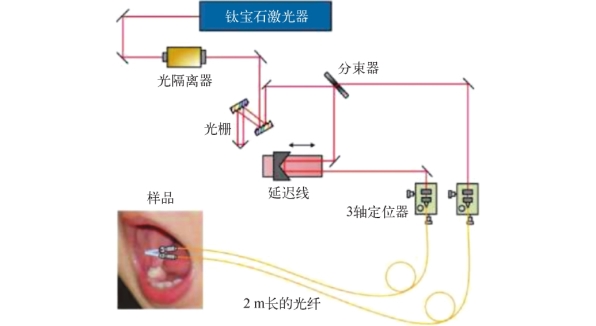
图7-8　基于亚波长塑料光纤的太赫兹内窥镜系统[56]

式中,I in和I out分别为输入和输出的光强度;d为样品厚度。我们认为,太赫兹在富含水的组织中的吸收由两部分组成：水和其他成分。吸收系数用下面的公式表述

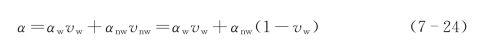
式中,αw和αnw代表水和其他成分对太赫兹波的吸收系数。v w和v nw为水和其他成分的体积分数,满足v w+v nw=1的关系。因此透射率公式可以写为

假设水的吸收系数比其他成分的吸收系数要高很多,因此除了干燥的样品,其他样品中的吸收都主要是由水分引起的。在富含水的样品中,其他成分对太赫兹波的吸收基本可以忽略,因此样品中水的体积分数可以表示为

从上式可以看出,水含量的体积分数的误差主要由透射率T和样品的厚度d决定。设A=ln T,那么v w的误差Δv ws可以写为

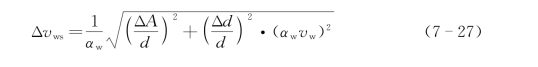
式中,ΔA和Δd分别是ln T和d的标准差。接下来的部分是有关测量不确定性的讨论。

首先,我们要考虑透射率的变化量与水含量体积分数变化量之间的关系。也就是说,在固定的样品厚度的条件下,计算误差是由透射引起的。体积分数的变化可以由式(7-25)得出

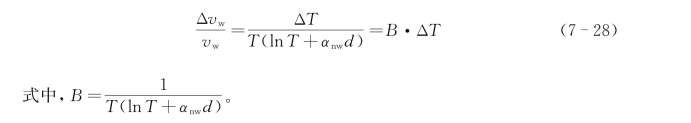
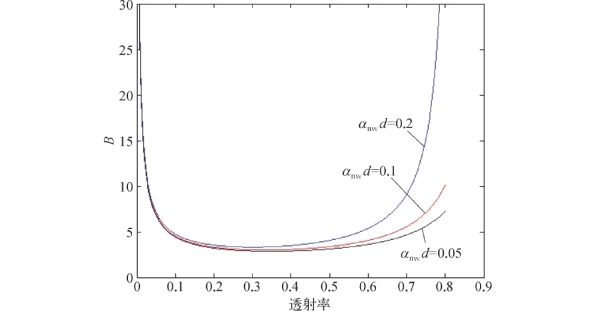
由于Δv w/ΔT总为负值,因此,-Δv w/(ΔT·v w)关于T的图像会得到最小相对误差的点,图7-9显示了水含量的误差与透射率之间的关系。

(www.xing528.com)

图7-9　水含量(体积浓度)误差和透射率之间的关系

由图7-9可知在透射率在0.2~0.6时,误差处于最小,而透射率在0.2~0.6之外时,引起的误差变化较大。因此应尽量保证透射率在0.2~0.6,避免误差的影响。另外,当αnw d越小误差值越小,当αnw d为0时,水分含量的相对误差有最小值T=36.8%。但是只要保证透射率处于0.2~0.6时,αnw d的变化引起的误差变化并不大。由文献可知,在低于2 THz的频率下,脱水的胃和肾脏组织的吸收系数一般小于20 cm-1。因此,样品的厚度应为几十微米的量级。而且样品厚度的选择原则应该保证αnw d处于一个相对较小的值,以尽量减小误差。另外,由于太赫兹波的穿透深度一般在波长量级,用于反射成像的样品厚度也不能太薄以保证样品与太赫兹波的充分接触作用。

在样品准备和成像测量的过程中,样品的厚度会存在误差以至于会影响接下来的透射率测量和水含量的计算过程。根据式(7 23),由样品厚度引起的透射率的变化可以表示为

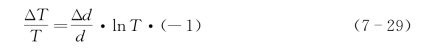
图7-10表述了由样品厚度引起的太赫兹波透射率的变化,可知太赫兹波的透射率对样品厚度的变化十分敏感。对于确定的Δd/d值,ΔT/T的值随透射率的增加对数降低,根据上述讨论,我们应该保证太赫兹波具有较高的透射率来减小误差。

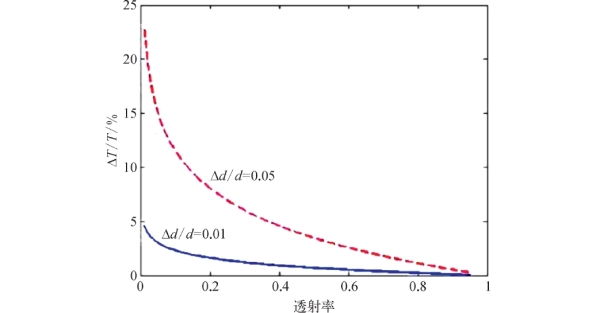
图7-10　太赫兹波透射率偏差与透射率之间的关系

另外,测量中生物组织中其他成分引起的吸收是被忽略的。因此,由于水的吸收造成的真实值与测量值之间的误差因子ε是应该估计的,可由下面的公式表示：

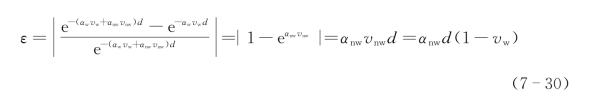
图7-11显示了当参数αnw d取值为0.05、0.1、0.2时,相对误差ε与水分体积分数之间的变化关系。因此,从图中可以清晰地看出,当样品厚度为微米量级、水分含量的范围在0.5~0.9时,样品透射率的相对误差ε小于5%。并且,当αnw d小于0.05时,即使水分含量很低,透射率的相对误差ε也小于5%。

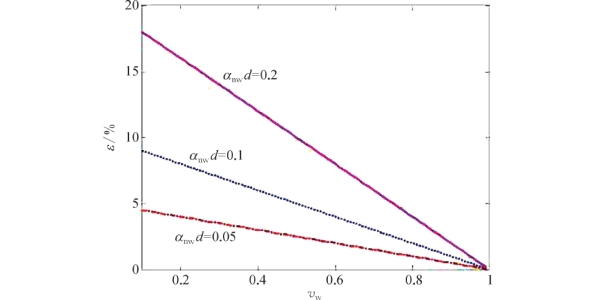
图7-11　水含量与透射率的误差值之间的关系

对于确定的透射率,不确定的水含量是由实验中样品厚度的误差造成的。所以,水分含量的变化Δv w可以表示为

可以看出Δv w和量测量准确性的主要影响因素。为减小样品厚度的误差,样品必须经过前期的严格制备,且较厚的样品有利于减小误差。呈线性关系。因此,样品的厚度就变成了实验中水含