生物组织太赫兹波段的吸收系数与折射率

从物质折射率和吸收系数计算介电常数通常采用K-K关系,其表达式为

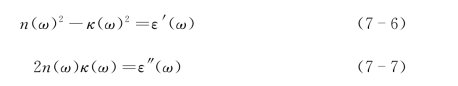
式中,n(ω)为折射率;κ(ω)为吸光系数;ε＇(ω)为介电常数的实部;ε″(ω)为介电常数的虚部。吸光系数和吸收系数的关系为[35]

式中,c为真空光速。

利用式(7-6)、式(7-7)和式(7-8)可以通过物质折射率和吸光系数(或吸收系数)计算得到其介电常数,但是无法反演。1996年,Kindt等[6]提出了一种利用物质介电常数近似计算吸收系数和折射率的方法,并实现了太赫兹波段物质折射率和吸收系数的计算,其表达式为

因此,利用介电常数也可以近似计算物质在太赫兹波段的吸收系数和折射率。利用介电常数的方法或者吸收系数和折射率的方法均可以用于表征生物组织在太赫兹波段的物理特性,并且可以相互反演。

到目前为止,物质的太赫兹波谱测量采用的最广泛的技术是太赫兹时域光谱技术,其测量方法可以直接获得物质在太赫兹波段的吸收系数和折射率。

脉冲太赫兹波的探测中,获得的是电场随时间的变化过程,记为E(t)。一个太赫兹时域脉冲中通常包含了半个到多个电磁振荡周期,而每个振荡周期对应的太赫兹脉冲一般从数十飞秒到皮秒。对太赫兹时域脉冲波形进行傅里叶变换可以得到对应的频域分布：

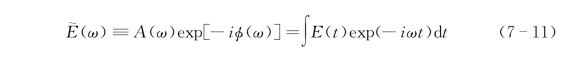
从式(7-11)中可以看出,太赫兹时域脉冲在频域是一个复数,描述了电场的振幅和相位。利用脉冲太赫兹技术测量物质在太赫兹波段的波谱信息的过程是直接测量了其电场强度,所以称之为太赫兹时域光谱技术,也是当前应用最广泛的太赫兹波谱测量的方法。利用该技术测量物质太赫兹波谱时,首先测量参考脉冲的时域波形,并对其进行傅里叶变换得到参考信号频谱A r(ω)exp[-iϕr(ω)],然后测量太赫兹脉冲经过样本后的时域波形,并对其进行傅里叶变换得到信号的频谱A s(ω)exp[-iϕs(ω)],利用测量到的参考频谱和信号频谱可以计算得到物质在太赫兹波段的吸收波谱和折射率,计算过程为

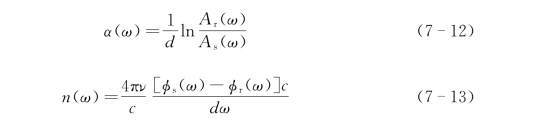
式中,α为吸收系数;n为折射率;d为样本的厚度;c是真空光速。

在当前的研究中,研究人员主要基于吸收系数和折射率分析生物组织在太赫兹波段的特性,由于不同生物组织折射率差异较小,并且利用折射率有时无法实现不同生物组织的鉴别,实际研究中,研究人员更多采用吸收系数对生物组织进行分析。另一方面,由于式(7-5)的介电模型主要表征太赫兹波在单一类型生物组织中的吸收和损耗,本文进一步采用非线性规划模型建立一种复杂生物组织的吸收模型。

假设基于式(7-5)的模型得到的不同类型生物组织在太赫兹波段的介电响应相互独立,则复杂组织中不同类型组织对太赫兹波的吸收则相互独立,在此基础上进行分析。对于两种生物组织情况,如图7-2所示,对于复杂生物组织,由于太赫兹波的波长远小于生物组织的尺度,因此忽略平面内太赫兹光斑同时覆盖多种组织的情况,实际中绝大部分区域出现的情况是太赫兹波透过多层交替重叠的单一类型组织,其整体的相位差可以通过不同层组织的相位差按一定比例的线性组合计算。先从两种类型生物组织重叠分析。

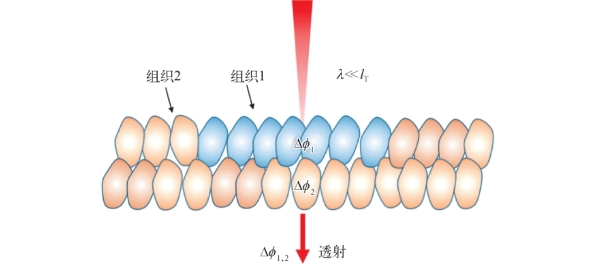
图7-2　太赫兹波在复杂组织中透射后的相位差

太赫兹波通过单一类型生物组织的相位差为

(www.xing528.com)

式中,n为折射率;d为样本的厚度;c为真空光速,则太赫兹波通过两层生物组织的总相位差可以表示为

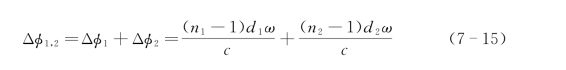
其等价于

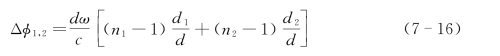
对照式(7-14),可得

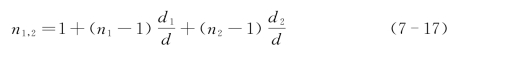
对于两层组织有d=d 1+d 2,因此,式(7-17)可以简化为

利用类似的方法,可以得到,吸收系数满足如下关系

因此,复杂生物组织在太赫兹波段的折射率可以通过各自单一类型组织的折射率按一定比例进行线性组合表示,并且其吸收系数特性也满足类似关系。

以乳腺癌组织对太赫兹波的吸收为例,其样本组织包含的组织类型包括正常纤维组织、脂肪组织和肿瘤组织,即待测生物组织主要由这三种类型组织混合而成。将图7-2所示的情况扩展到三种生物组织,则复杂生物组织的吸收系数可以表示为

式中,c 1~c 3为系数且和为1;αN、αF、αC分别为纤维组织、脂肪组织和肿瘤组织在太赫兹波段的吸收系数。

式(7-20)所示复杂生物组织太赫兹波吸收模型参数的求解可以等价为一种数学规划模型,即

式中,αm为实际测得的太赫兹吸收波谱。值得指出的是,式(7 21)看似是一个线性规划问题,但是由于αN、αF、αC是不同频率下不同类型生物组织对太赫兹波的一系列吸收系数,因此每个吸收项均是列向量,无法用传统的线性规划模型进行求解。这里将其转化为一个等价的非线性规划问题,则式(7-21)的问题可以转化为

式中,ω1~ω2为太赫兹吸收波谱的范围,原始波谱的频谱分辨率越高,拟合将会越精细。式(7-22)为典型的多元二次多项式的非线性规划模型。