光学太赫兹辐射源及其生物医学应用

差频技术是最早于20世纪60年代提出的产生太赫兹的技术,最近三十多年得到了长足的发展,不断有新的成果出现,成为目前太赫兹产生的重要技术之一。利用非线性差频可以产生功率较高的相干、可调谐单频太赫兹波,这在材料科学、固体物理、生物科学、高频谱分辨率的分子光谱、射电天文、通信等基础研究和应用研究领域具有重要研究价值和实用意义。

差频技术产生太赫兹辐射的最大优点是没有阈值,实验设备简单,结构紧凑。与光整流、光电导以及光混频技术产生太赫兹相比,可以获得较高功率、窄带太赫兹波辐射,且不需要价格昂贵的泵浦装置。对于利用差频技术的太赫兹辐射源来说,双波长激光器与非线性增益介质的选择和研究至关重要,不仅关系到太赫兹辐射源输出波长的覆盖范围,还影响着激光器的输出功率以及能量转换效率等。为了获得较高效率的太赫兹波输出,需要选择合适的差频材料。选择应用于太赫兹波频段的非线性晶体的条件是：①在所作用的波段范围内具有较高的透射率;②具有高的损伤阈值;③具有高的光学质量;④具有大的非线性系数;⑤优秀的相位匹配能力;⑥晶体可以大尺寸地生长。差频过程中的相位匹配是决定辐射源输出功率和转换效率的重要因素。选择在差频晶体中可满足相位匹配条件,且输出功率高、波长比较接近的差频泵浦光(两波长间隔视其所在波段范围所定,一般在十几个纳米左右),从而理论可获得调谐范围较宽的相干窄带、高功率的太赫兹波输出。

差频的动力学过程可以用高斯模型[1]和平面波[2]模型来分析。若波长与光束的尺寸可以相比拟、衍射作用不能忽略时,这时就需要用高斯模型并考虑到光束的有效截面、聚焦和吸收等因素来进行准确的分析,但是其中涉及傅里叶积分变换,计算较为烦琐。若当光束直径与波长比a/λ≫1的情况下,无限平面波在半无限介质中沿z方向上差频也能给出很好的近似。差频产生太赫兹波的原理如图5-1所示,两个频率相近的激光ωp1和ωp2在非线性晶体中差频产生太赫兹波输出,即ωp1-ωp2=ωTHz,其中χ(2)为二阶非线性极化强度。为了分析差频产生太赫兹波的输出特性,假设ωp1、ωp2和ωTHz三波均为平面波,并且均沿z方向传输,其电场强度用下式来表示：

图5-1　差频产生太赫兹波的原理示意图

其中k p1、k p2和k THz分别代表频率ωp1、ωp2和ωTHz三波波矢;αp1、αp2和αTHz分别代表三波在非线性晶体内的功率吸收系数。值得的注意的是,由于目前差频产生太赫兹波所用的非线性介质均在太赫兹波和近红外波段内有较强的吸收,因此此处的吸收作用不能忽略。这样,非线性介质内总的电场强度为

将式(5-2)代入麦克斯韦方程,得到如下的方程：

式中,σ为介质的电导率张量;μ0为真空中的磁导率;ε=ε0(χ(1)+1)为介电常数张量;P NL为非线性极化强度。将差频ωTHz非线性极化强度分量改为标量形式：

令σ=0,并采用慢变振幅近似,即在空间约化波长的范围内,振幅的变化很小,可以忽略,得到耦合波方程：

利用P NL,我们可以得到E THz的空间形式如下：

同样可以得到：

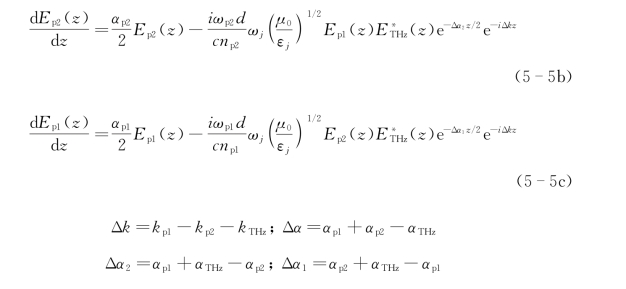
式中,Δk为三波间的相位失配量;c为真空中的光速;n p1、n p2和n THz分别为三波的折射率;d=χ(2)/2为最低阶的非线性系数。

假设注入晶体中差频的两波ωp1和ωp2的幅度衰减可以忽略不计,即在小信号情况下,认为整个晶体内E 1(z)和E 2(z)是常数,则对式(5-5a)在整个晶体长度内积分,可以得到晶体出射表面内侧的电场强度：

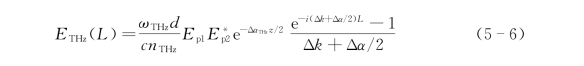
式中,L为晶体的长度。通过光强I THz与电场E THz的关系：

将式(5-6)代入式(5-7),可以得到

当不考虑晶体的吸收时,式(5-8)可以简化为

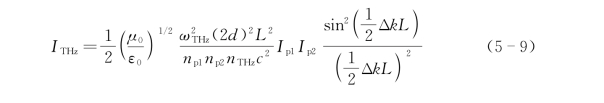
当晶体的端面未镀膜,特别是当晶体的表面法线不与z轴平行时,菲涅耳损耗更为严重,因此,当考虑到两波ωp1和ωp2在晶体入射端面及太赫兹波在出射端面的菲涅耳损耗时,太赫兹波的输出功率可以表示为

式中,A为光束横截面积;T p1、T p2和T THz分别为ωp1和ωp2在晶体入射端面及太赫兹波在出射端面的菲涅耳损耗。式(5-10)即为在平面波条件下共线差频产生太赫兹波输出功率的小信号近似解。

若ωp1和ωp2两波在差频过程中的振幅衰减不能忽略,就需要求解式(5-5)的数值解。

将ωp1、ωp2和ωTHz波复振幅的实部与虚部分开,令：

代入式(5-5),则有

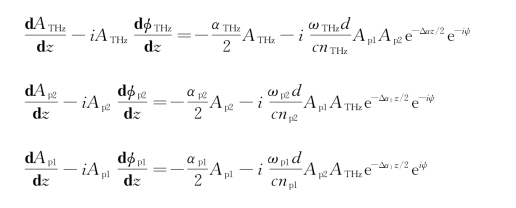
式中,ψ=Δkz+ϕp1-ϕp2-ϕTHz,为相对相位角。

进一步分离可以得到以下方程组：

当满足相位匹配条件Δk=0时,差频过程中的转换效率与相对相位角初始值ψ(0)无关,并且在差频的过程中相对相位角保持ψ=-90°,据此可以使式(5-12)进一步简化。

利用数值方法可以对上述微分方程组(5-13)进行求解,假设注入非线性介质中的两波ωp1和ωp2的波长分别为1.061μm和1.067μm,光功率密度均为6.6 MW/cm2,相位匹配条件Δk=0,则产生的波长为189μm的太赫兹随作用长度的变化如图5-2所示。为了便于观察分析,没有考虑晶体的吸收效应。

图5-2　差频过程中三波光强随传输距离的变化

从图5-2可以看出,能量随着传输距离的变化在三波间转化,ωp1的能量减小,而相应的ωp2的能量和ωTHz的能量相应增加。根据Manley Rowe三电场之间功率交换的关系式[3]：

其中的ΔP表示在给定频率下功率的变化,对于频率ωp1-ωp2=ωTHz的差频产生,Manley Rowe关系式指出,在ωp1处的功率耗费在所产生的ωTHz的太赫兹波上和向ωp2的能量的转移上,因此,差频的本质是在ωp1处的功率到其他较低频率能量的转移,或者是低频率成分参量放大的过程。在光子的概念中,一个频率为ωp1的光子分成频率为ωp2的光子和太赫兹波光子。按照Manley-Rowe关系式,差频过程中最大的量子效率由下式决定：

它相当于100%的量子效率,因此,当注入的波长为1.061μm时,差频产生1.59 THz(189μm)的最大量子效率也仅为0.56%,从图5 2也可以看出当作用距离为50 mm时效率为0.158%,在实际过程中,受非线性介质的吸收和边界效应等因素的影响,差频效率会更加低。(www.xing528.com)

从式(5-9)中可以看出,当Δk→0时,差频产生太赫兹波的光功率密度I THz正比于晶体的长度的平方：I THz∝L 2。当Δk=0时,式(5-10)可以简化为

其中Fα为由于晶体吸收而增加的修正因子：

由于非线性介质在太赫兹波段的吸收系数较大,使得晶体的有效作用长度变短。图5-3给出了在I p1和I p2均为6.6 MW/cm2、αp1和αp2为0.2 cm-1的情况下,在不同晶体吸收系数下产生太赫兹波随作用长度的变化情况。从图5-3中可以看出,在没有晶体吸收的情况下,太赫兹波的功率密度是与作用长度平方成正比的,在存在吸收的情况下,晶体存在一个最佳长度,并且随着晶体吸收系数的增加,最佳长度是减小的,同时最佳长度处对应的峰值光功率密度也是减小的。

图5-3　在不同晶体吸收系数下产生太赫兹波随作用长度的变化

若非线性介质在近红外波段的吸收远小于在太赫兹波段的吸收,可以认为αp1=αp2=0,则Fα修正因子变为

在αTHz L≪1的情况下,按照泰勒级数展开,Fα修正因子可以简化为1;在αTHz L≫1的情况下,其变为Fα=(2/αTHz L)2,这意味着晶体的有效作用长度为2/αTHz,在这种情况下,它与实际晶体的长度无关。图5-4表示在晶体长度为10 mm、25 mm和50 mm的情况下,产生的太赫兹波光功率随吸收系数的变化情况,可以看出晶体的吸收对长晶体的影响较为大。

图5-4　太赫兹波光功率随吸收系数的变化

不同的差频晶体具有不同的晶体结构特性,因此要合理选择相位匹配方式来获得太赫兹波辐射。按照互作用的三波波矢是否共线,可以分为共线的相位匹配和非共线的相位匹配方式,若互作用的三波波矢共线,设参与差频过程的三波长分别为λp1、λp2和λTHz,其波矢分别为k p1、k p2和k THz,根据动量守恒,在完全满足共线相位匹配条件时,有

即

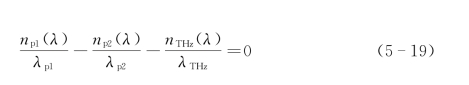
根据差频过程中的能量守恒式：

并根据单轴晶体中,e光折射率的表达式为

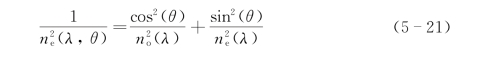
如果实际注入的两波长λp1、λp2有一定线宽和发散角的存在,完全相位匹配条件往往不能完全满足,即Δk≠0,此时按照式(5-8),当|Δk|≤π/L,太赫兹波输出功率降为最大值的40.5%,这时的相位失配量还是允许的,在不考虑晶体吸收的情况下,可以根据此条件来计算允许线宽和相位匹配允许角。

在只考虑晶体对太赫兹波吸收的情况下,太赫兹波输出功率随相位因子Δk L的变化情况如图5 5所示,可以看出,在相同晶体长度的情况下,随着晶体对太赫兹波吸收增大,太赫兹波的输出功率降低的同时,功率下降为最大输出值的40.5%时允许的相位失配因子也增大,从而导致允许线宽和允许角的增大。图5-6展示了允许的相位失配因子随吸收因子αTHz L的变化情况,当αTHz L=0,即不存在晶体的吸收时,相位失配允许量为|Δk|≤π/L,当αTHz L=7时,相位失配允许量变为|Δk|≤1.5π/L。

图5-5　归一化太赫兹波强度随相位失配量的变化情况

图5-6　相位失配允许量随晶体吸收因子αTHz L的变化

设相位匹配角为θp,泵浦光的允许角为Δθ,三波波矢的方向为θ=θp+Δθ。相位失配因子

将相位失配因子在Δk在Δθ=θp处泰勒级数展开,得到的单轴晶体相位匹配允许角的计算式,如式(5-23)所示,当考虑到晶体的吸收时,可以相应的加入修正因子。在双轴晶体中还应计算方位角的允许变量。

同样可以得到允许线宽的计算式如下：

图5-7展示了双波长分别为1μm附近和2μm附近,通过1 cm长度的GaSe晶体差频时的相位匹配允许角,可以看出,允许角随着频率的增大而减小,并且2μm的双波长差频时具有稍大允许角,例如,1.5 THz时,它们的允许角分别为0.44°和0.38°。

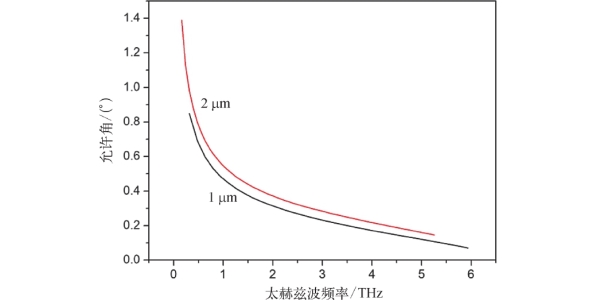
图5-7　GaSe o-ee类相位匹配允许角随输出频率的变化

同样可以得到o-ee类相位匹配的允许线宽值,GaSe晶体的长度为10 mm,如图5-8所示。可以看出,采用1μm附近的双波长差频和采用2μm附近的双波长差频,它们的允许线宽也均随太赫兹波频率的增大而减小,并且2μm附近的双波长差频时具有较大的允许线宽。由于注入晶体的双波长的频率接近,因此可以认为它们有相同的允许线宽,不同的偏振状态对它们的影响较小。

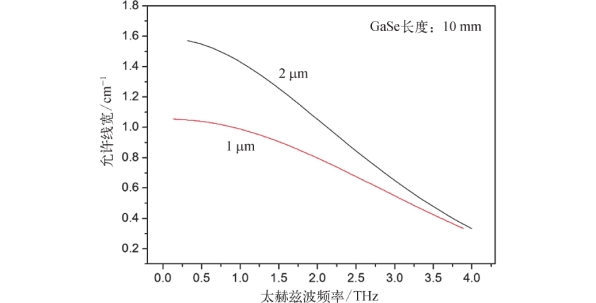
图5-8　长度为10 mm的GaSe晶体差频的允许线宽

有些差频晶体为各向同性化合物,不存在双折射效应,因此无法利用双折射来实现相位匹配,这些晶体剩余辐射带两侧的折射率存在较大的差异,因此可以利用剩余辐射带两侧的色散补偿来实现非共线的相位匹配。

若互作用的三波的波矢分别为kλ1、kλ2和k THz,波矢方向如图5-9所示,注入晶体内的双波长的波矢夹角为θ,产生的太赫兹波的波矢k THz与kλ2的夹角设为φ。根据几何关系可以得到[13]：

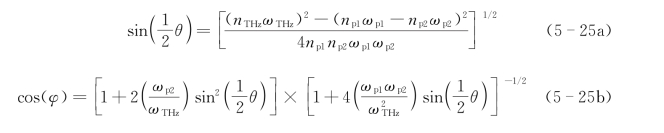
其中n p1、n p2和n THz分别是圆频率为ωp1、ωp2和ωTHz的折射率,并结合差频晶体的色散方程,可以得到波矢夹角。当λp1=1.95μm,λp2在1.957~2.020μm内变化时得到在GaAs的匹配曲线如图5-10所示,理论上可以产生0.55~5.33 THz的太赫兹波输出,可以看出θe角度较小,变化范围为0.21°~3.20°,因此注入的双波长的夹角调整精度要求较高,φ角的变化范围为16.7°~24.9°,为了减小产生的太赫兹波在出射端的菲涅耳损耗,可以将出射面切割成约20°斜面。

图5-9　非共线三波波矢示意图

图5-10　GaAs晶体非共线差频匹配角