晶格振动模三波耦合作用的理论研究成果

在这一节,我们将根据Henry和Garrett以及Sussman[20]等的理论研究工作,对在受激电磁耦子散射中三波互作用的机理进行理论分析,并推导出在此受激散射过程中太赫兹波和Stokes光的增益系数和吸收系数的表达式。

简单起见,我们假设泵浦光、Stokes光和太赫兹波的电场E以及晶格振动位移场Q均为单色平面波,则有

和

式中,β=p、s、T分别代表泵浦光、Stokes光和太赫兹波为增长或衰减常数;c.c.表示复共轭。

在上一节提到的耦合波方程式(4-4)、极化方程式(4-5)以及运动方程式(4-6)中,极化项是线性的,所以耦合波方程亦为一线性微分方程。对于非线性频率变换过程,极化项不仅具有线性项,还具有非线性项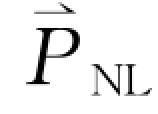。这时,非线性耦合波方程变为

而此时多振动模物质的第j个振动模的运动方程变为

式(4-17)中,右边驱动力项分为两个部分：线性部分和源自散射过程的非线性部分。根据Kleinman[21]首次提出的能量密度方法,该过程中的能量密度函数可写为

式中,d E和d Q为物质的非线性系数,在后面的分析中我们可以看到d E项与非线性极化过程中的参量过程有关,而d Q则源于极化过程中的振动过程。

根据能量密度函数推得的非线性驱动项分别为(www.xing528.com)

和

将式(4-19)和式(4-20)代入式(4-4)和式(4-17),可得

考虑一定的边界条件,通过求解方程组(4-21),就可完全描述该受激散射过程。为了进一步了解该作用过程,我们求解式(4-21d)中的Qj(ωT),得到

并假设在作用过程中泵浦光无衰减损耗(=0),将式(4-22)代入式(4-21a)和式(4-21b),则有

下面我们来分析式(4-23c)中右边其中两项的重要物理意义。

第一项d＇E E(ωp)E(ωT)*,它是典型的与参量过程有关的非线性极化项,其仅与两电磁场的乘积有关,而与任何晶格振动模都无关。在E(ωT)为最大值的区域,该项具有最大值。而发生此现象时的区域就是最低振动模的电磁耦子色散曲线的类光子特性部分,在该区域电磁耦子的绝大部分能量是电磁特性的,并且此时对闲频光或太赫兹波的吸收较小。因此,色散曲线的类光子部分也称为参量作用区。

最后一项,它是常见的拉曼极化项,其与泵浦光场和晶格振动位移的乘积有关,而与闲频光场E(ωT)的存在无关(也就是说在非红外活性物质中也成立)。当振动位移Q(ωT)较大时,此拉曼项占主导地位,对应色散曲线的类声子区域。另外,当ωT等于TO模本征频率ω0j时,该项具有最大值,从而此时纯拉曼增益在ωs=ωp-ω0j时达到最大值。这时,频率ωs即为通常所能观察到的Stokes光散射频率。因此,色散曲线在类声子部分也被称为拉曼区。