晶格振动可以分解成若干简单的振动,每一种振动方式叫作振动模,用频率ω和波矢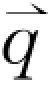 来表示。光波和声波的频率ω与波矢
来表示。光波和声波的频率ω与波矢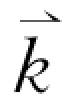 之间为线性关系,而晶格振动的频率ω与波矢
之间为线性关系,而晶格振动的频率ω与波矢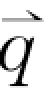 之间的关系并不是线性关系。晶格振动的ω-
之间的关系并不是线性关系。晶格振动的ω- 之间的关系构成了晶格振动的特征色散关系。
之间的关系构成了晶格振动的特征色散关系。
从上一章可知,对于简单的双原子复式格子,存在两种独立色散关系的格波,分别为频率较高的光学波支和频率较低的声学波支。对于声学波,相邻不同种原子振动方向相同,在布里渊区中心附近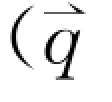 →0)时声学波实际上代表原胞质心的振动,不仅相邻原胞中原子振动的相位差趋于零,而且振幅也近乎相等。而对于光学波,情况正好相反,相邻不同种原子振动方向相反,振动过程中原胞的质心保持不动。如果相邻原子分别具有正、负不同种电荷,那么这种振动模可以吸收或产生与晶格振动频率相同的电磁辐射,这时我们称该模具有红外活性。具有红外活性的晶格振动模可以在介质中与具有相同或相近频率的电磁波发生耦合,不仅会改变该电磁波在介质中的传输特性,而且在接近共振频率处晶格振动模的色散曲线也将发生明显变化。
→0)时声学波实际上代表原胞质心的振动,不仅相邻原胞中原子振动的相位差趋于零,而且振幅也近乎相等。而对于光学波,情况正好相反,相邻不同种原子振动方向相反,振动过程中原胞的质心保持不动。如果相邻原子分别具有正、负不同种电荷,那么这种振动模可以吸收或产生与晶格振动频率相同的电磁辐射,这时我们称该模具有红外活性。具有红外活性的晶格振动模可以在介质中与具有相同或相近频率的电磁波发生耦合,不仅会改变该电磁波在介质中的传输特性,而且在接近共振频率处晶格振动模的色散曲线也将发生明显变化。
下面我们将从理论上简单介绍具有红外活性的晶格振动模的色散特性。通常,耦合波方程可写为
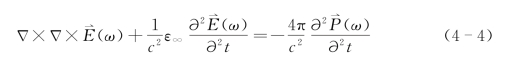
式中,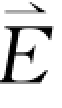 (ω)和
(ω)和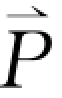 (ω)分别表示在频率为ω时的电场和极化强度;c为光速;ε∞为与频率无关的高频介电常数。由于在实验中,三波的偏振方向都平行于晶体的光轴方向,而极化矢量亦平行于泵浦光偏振方向,因此上述耦合波方程就可简化为标量方程。简单起见,在这里我们只考虑单一振动模时的情形,其结果可以推广到多振动模情况。
(ω)分别表示在频率为ω时的电场和极化强度;c为光速;ε∞为与频率无关的高频介电常数。由于在实验中,三波的偏振方向都平行于晶体的光轴方向,而极化矢量亦平行于泵浦光偏振方向,因此上述耦合波方程就可简化为标量方程。简单起见,在这里我们只考虑单一振动模时的情形,其结果可以推广到多振动模情况。
在光电场作用下,介质中的电荷会在电场的作用下产生移动,这种在外电场作用下介质体系内部电荷的移动将会产生相应的电极化强度,简而言之,介质的极化源自外电场作用下介质中电荷的位移。在简谐近似情况下,极化强度和电子振动偏离平衡位置的位移之间有如下关系:
![]()
式中,e为与横向振动有关的电子电荷;N为单位体积内原胞的粒子数;Q为振动粒子偏离平衡位置时的位移。则运动方程可表示为
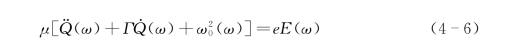
式中,μ为振动粒子的折合质量;ω0为晶格振动的本征共振频率;Γ为阻尼系数。
假设E(ω)、P(ω)和Q(ω)都以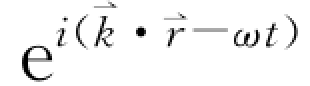 的形式变化,则式(4-4)、式(4-6)可分别改写为
的形式变化,则式(4-4)、式(4-6)可分别改写为
![]()
和
![]()
式中,D(ω)=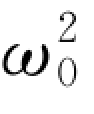 -ω2-iΓω。根据式(4-5)和式(4-8)可以求解得到(https://www.xing528.com)
-ω2-iΓω。根据式(4-5)和式(4-8)可以求解得到(https://www.xing528.com)

将式(4-9)代入式(4-7),则可得到色散方程

定义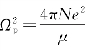 ,则上述色散方程可以改写为
,则上述色散方程可以改写为
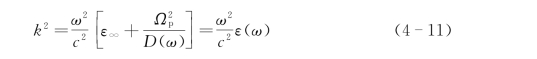
图4 5是根据式(4 11)计算得出的单振动模电磁耦子色散曲线示意图。定义波矢k=k'+ik″,其中k的实部Re(k)=k'(图中右侧部分)为传播常数,表示电磁波的色散,虚部Im(k)=k″表示电磁波的吸收。从图4-5中可以看出,传播常数k'随着频率的变化而改变,吸收常数α=2k″在频率ωTO处共振增强,而在ω→0时趋于零。
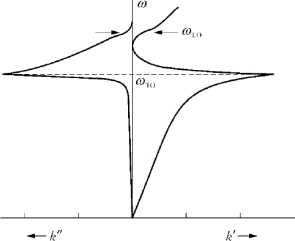
图4-5 单振动模电磁耦子色散曲线示意图
ωTO—横向光学模;ωLO—纵向光学模
上面分析的是单振动模的情况,而对于具有多振动模介质的情形,式(4-9)变为
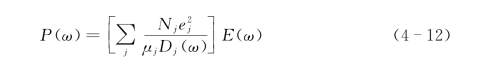
同时色散方程式(4-11)变为
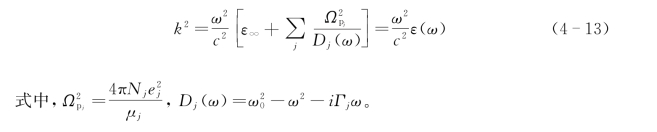
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




