垃圾填埋场防渗新技术及其数值分析成果

1）渗流微分方程及有限元形式

假定土和水不可压缩，将达西定律与连续性方程联立可得到稳定渗流微分方程：

在渗流微分方程的基础上，使用加权余量的伽辽金法可将微分方程转化为线性方程组，从而得到渗流方程的有限元形式：式中　——渗透系数的分量；

α——渗透方向与水平面的夹角；

H1，H2——节点水头；

＜N＞——插值函数向量，对其的偏导分别为水平及竖直方向的单位梯度；

q——边界流量；

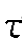——单元厚度，瞬态渗流时λ为mwγw；

t——时间；

A——单元面积之和；

L——边界长度之和。

在分析稳态渗流时不需要考虑时间因素，即第二项中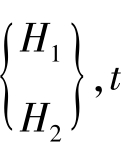为0，此时式（8.2）为：

式（8.3）为稳态渗流方程的有限元形式。

2）计算模型及参数

根据室内模型箱的尺寸建立有限元分析模型，取PBFC浆材浇筑的防渗墙有关计算参数为：压缩模量Es=200 MPa、水平渗透系数kH=4.6×10-10m/s、含水量θ=70.1%。

根据实验情况，水位保持在墙高0.7 m左右，因此需将渗流类型设置为饱和/非饱和渗流进行分析。若采用完全饱和状态分析会导致分析的结果中浸润面以上的非饱和区域也有大量渗径，而实际浸润面以上仅有少量渗径产生，这样会使得分析结果产生比较大的偏差。在模型设计时考虑溶液的水压力可能对墙体造成变形或压缩，在实验过程中已在墙体两侧加装了模板以抵消静水压力的影响。假定防渗墙始终处于理想状态，即没有形变或位移的产生，同时设渗流箱内为一个封闭系统，与外界不会有水分交换。

根据试验确定数值分析模型中各材料的尺寸，其中防渗墙高1 m，墙厚0.08 m，溶液共计300 L，根据箱体尺寸计算得出水位高度0.7 m。模型计算简图如图8.6所示，网格划分类型采用四边形（或三角形）网格模式，网格单元尺寸设为0.01 m比较适合。水头边界类型选择水头高度，设置左水头边界为水头高度0.7 m，右水头边界为水头高度0 m。其中模型箱使用了槽钢及插板以改变近水面面积的大小，由于槽钢及插板均不透水可将其视作截流幕墙，需定义隔水边界来模拟。隔水边界可通过选择总流量的边界类型（设置总流量为0）来模拟。以加装插板时为例，模型网格划分与边界设置如图8.7所示，其中三角形边界为隔水边界。

为了探究迎水面积对渗流的影响，这里设置了两个工况来进行模拟研究，分别为工况1：加装插板；工况2：不加装插板。

图8.6　模型简图

图8.7　网格划分及边界设置

3）工况1：加装插板计算分析

（1）渗透速度与比降分析

当墙侧插板长度为0.3 m时，除去槽钢面积后模型箱中PBFC改性防渗墙的迎水面积为0.192 m2，模拟分析出的水头云图及浸润线、孔隙水压力云图分别如图8.8、图8.9所示，渗流矢量分布如图8.10所示。

图8.8　总水头云图及浸润线

图8.9　孔隙水压力云图

图8.10　渗透矢量分布图

图8.11　孔隙水压力变化(www.xing528.com)

根据等势面的分布情况，水头及孔隙水压力较高的区域主要集中在防渗墙底部，数值随着墙高的增加及渗透距离的增长而逐渐减小。由于安装插板的缘故，近水面孔隙水压力在墙高0.4 m处发生了快速下降的情况。如图8.11所示，孔隙水压力的变化范围为-10～6 kPa，远小于防渗浆材的设计抗压强度，说明安全性很好。渗透矢量的长度代表着渗透速度的大小，渗透矢量的方向代表着渗透水流的流向，可见其渗流主要以水平方向流动为主。

如图8.12所示，渗透速度集中在防渗墙高0.08～0.4 m处，渗透速度随墙高增加大致呈减小趋势。墙高0.08 m以下的部分数值较低，而墙高0.4 m以上的部分数值则快速趋向零，这是由于此范围内的插板及槽钢为不透水材料导致的。其中远水面渗透速度最大值为3.86×10-9 m/s，出现于墙高0.22 m处；近水面最大渗透速度出现在0.09 m处，最大值为1.34×10-8 m/s。如图8.13所示，渗透比降在墙高0.28 m处取得最大值9.46，满足安全标准。同时在实验过程中未发现模型墙体出现明显变形及渗透破坏的情况，说明PBFC改性防渗墙在使用中可以保持完整性与连续性。这样既可以阻隔垃圾及渗滤液与外界的接触，也可以充分吸附渗滤液中的有害物质。

图8.12　防渗墙面渗透速度

图8.13　防渗墙渗透比降

（2）渗透量对比分析

在墙体远水面绘制一个过流断面，该断面模拟分析得出的流量即为人工配制的模拟溶液穿透防渗墙后的渗透量。防渗墙远水面的过流断面流量为1.27×10-9 m3/s，考虑墙的长度为0.7 m，因此根据分析结果计算出模型墙单位长度内的流量为8.89×10-10 m3/s，与实测值的对比如图8.14所示。

图8.14　渗透量模拟值与实测值的对比

由数值分析得到的日均渗透量为76.8 mL/d，收集的渗透量实测值在开始几天内约为150 mL/d，随着时间的变化快速减小并在5 d后稳定在40～50 mL/d，每日渗透量实测值均值较5 d前的平均值降低了38.1%。从总体来看，实测值与模拟值的变化趋势基本一致。实测值初期偏大，这是由于防渗浆材在养护后一段时间内其内部材料因失水发生收缩而拓宽了渗流通道或墙体产生细微裂隙，使得渗流过程前期出现了渗透系数偏大的情况。而模拟分析使用的渗透系数则为对完全饱和状态下的试样进行实验测得的数据，因此会出现渗流量实测值大于模拟值的情况。

对于实验的中后期，实测值逐渐稳定并小于模拟值，是由于随着渗流的进行墙体材料中的膨润土吸水重新膨胀，使墙体中的裂隙与渗流通道的大小逐渐恢复正常，日均渗透量逐渐变小且变化趋势趋于稳定；由于模拟分析为绝对理想状态，而实际实验中不可避免地会出现水分损失的问题，在天气炎热时影响更大，这会造成一定的误差。同时在收集渗滤液的过程中会有部分水分残留在集液槽内，也会导致实测值存在误差。

4）工况2：加装插板计算分析

（1）渗透速度与比降分析

未加装插板时，除去槽钢面积后模型箱中PBFC改性防渗墙的迎水面积为0.372 m2，模拟分析出的水头云图及浸润线、孔隙水压力云图如图8.15、图8.16所示，渗流矢量分布如图8.17所示。

图8.15　总水头云图及浸润线

图8.16　孔隙水压力云图

图8.17　渗透矢量分布

图8.18　孔隙水压力变化

当防渗墙近水面没有安装插板时，可见水位以下的墙体内部均有渗流产生。总水头与孔隙水压力的等势面分布情况与工况1的分析结果类似，此时渗透矢量的方向仍以水平为主。如图8.18所示，孔隙水压力的范围在-10～6 kPa，也在防渗浆材的设计抗压强度范围之内，说明PBFC防渗浆材浇筑的墙体可以很好地满足垃圾填埋场的要求。

如图8.19所示为渗透速度曲线分布情况，渗透速度主要分布在墙高0.08～0.7 m处，渗透速度随墙高增加而减小。除去因交界处材料属性剧变而出现的特异值，防渗墙近水面渗透速度峰值出现在墙高0.13 m处，数值为4.67×10-9 m/s。防渗墙远水面渗透速度峰值出现在墙高0.25 m处，数值为3.72×10-9 m/s。由于模型尺寸偏小的缘故，墙面两侧渗透速度的峰值并没有发生明显的变化，但远水面渗透速度峰值的位置较工况1上移了0.03 m，说明迎水面积越大渗透作用越明显。

如图8.20所示，渗透比降最大值为9.90，出现于墙高0.56 m处，此时防渗墙的渗透比降也处于安全范围之内。当不加装插板时，其渗透速度和渗透比降的数值及变化规律与工况1的分析结果类似，由于迎水面积较大，因此数值相对工况1要大一些。除去因边界材料属性突变而导致的软件分析产生的误差点，在没有插板遮挡的区域内渗透速度与渗透比降变化平缓均匀，因此可认为防渗墙和易性较好，具有良好的工程性能。

图8.19　防渗墙面渗透速度

图8.20　防渗墙渗透比降

（2）渗透量对比分析

防渗墙远水面过流断面流量为2.44×10-9 m3/s，考虑墙的长度为0.7 m，根据分析结果计算出模型墙单位长度内的流量为1.72×10-9 m3/s，与实测值的对比如图8.21所示。

图8.21　渗透量模拟值与实测值的对比

数值分析得到的日均渗透量为148.61 mL/d，收集的渗透量实测值在开始几天内约为280 mL/d，随着时间的变化快速减小并在5 d后稳定在100～110 mL/d，每日渗透量实测值均值较5 d前的平均值低了57.3%。日均渗透量的变化趋势与工况1一致，在不考虑误差的情况下初期渗透量会迅速减小并在一段时间后趋向一个固定范围，说明垃圾填埋场防渗墙在投入使用后会迅速提升渗透性能，其防渗能力在一段时间后达到稳定。