非线性模型分析与建立

1）ANSYS软件及其分析过程

（1）ANSYS软件简介

ANSYS软件是由美国开发的通用型有限元分析软件，其开发范围包括流体、结构、电磁场等，可以和多种CAD连接，实现资源共享，如Pro/Engineer，NASTRAN，Alogor，I-DEAS，AutoCAD等，是现代产品设计中的高级CAE工具之一。ANSYS技术的种类有很多，其中包括有限元法（Finite Element Method，FEM）、边界元法（Boundary Element Method，BEM）、有限差分法（Finite Difference Element Method，FDM）等。ANSYS分析也有一定的局限性，许多方面（如渗流、水腐蚀等）无法建模，有待解决。对坝体的渗流方面其稳定性的影响比较小，基本可以忽略。因此，进行垃圾填埋场防渗墙应力变形分析时，忽略了渗流影响。

（2）ANSYS有限元法的分析过程

有限元法是将结构整体进行离散分析，形成有限个相连的单元，通过建立单元中以结点位移为基本未知数的函数，进而进行组合构造出整体结构函数进行求解。其具体分析过程如下所述：

①结构离散化。即将所分析问题的结构划分为有限个单元体，并在其指定位置设置节点，使相邻单元的有关参数具有一定的连续性，形成有限元网格。划分单元的大小和数量应根据计算精度和计算机容量等因素确定。

②选择位移差值函数。为了能用节点位移表示单元体位移、应变和应力，选择适当的位移函数是有限元分析中的关键。位移矩阵为：

式中　{f}——单元任意一点的位移；

{δ}——单元节点位移；

[N]——行函数。

③分析单元的力学特性。先用几何方程推导出用节点位移表示的单元应变：

式中　{ε}——单元应变；

[B]——单元应变矩阵。

单元应力通过根据本构方程推出的节点位移可表示为：

式中　[D]——与单元材料相关的弹性矩阵。

最后由变分原理可得单元上节点力与节点位移间的关系式（即平衡方程）：

式中　[k]e——单元的刚度矩阵：

④集合所有单元的平衡方程，建立整体结构的平衡方程。即将各个单元的刚度矩阵合成整体刚度矩阵，然后将各个单元的等效节点力列出矩阵，集合成总的荷载列阵。

⑤由平衡方程求解未知点位移和计算单元应力。

2）材料的本构模型

在岩土工程有限元分析中，主要是材料的应力-应变-强度-时间关系，为准确描述岩土材料的力学特性，国内外学者进行了大量的实验和理论研究，使有限元理论不断发展，许多材料的本构模型被提出并被验证，根据不同的本构模型对材料力学特性的概括，本构模型主要分为四类：线弹性本构模型、弹性非线性本构模型、弹塑性本构模型和其他力学本构模型。

（1）线弹性本构模型

在材料的本构关系中最基本、最简单的即为线弹性本构模型，这种模型是在一定的假定条件下组成的，材料的应力应变为线性关系，无论加荷还是卸荷均沿同一直线变化，并且完全卸载后无残余变形，弹性模量为常量，应力与应变有确定的唯一关系，即符合广义胡克定律，其刚度矩阵为：

胡克定律中包含了3个弹性常数，分别是弹性模量E、横向变形系数（即泊松比ν）和剪切模量G，且由于因此独立的弹性常数只有两个，一般以E和ν表示。

（2）弹性非线性本构模型

弹性非线性本构模型，即应力与应变为非线性的关系，该本构模型应用于混凝土材料的主要有两种，即Ottosen和Darwin-Pecnold。对于不同类型的土的弹性非线性模型最常用的为邓肯（Duncan）和张（Chang），依据三轴仪应力应变实验结果提出的双曲线模型。Duncan-Chang模型的基本参数为切线杨氏模量E和切线泊松比ν，计算式为：

其中，　

式中　K，n——试验常数；

Pa——大气压；

c——水泥土体的黏聚力；

φ——水泥土体的内摩擦角；

σ1-σ3——主应力差；

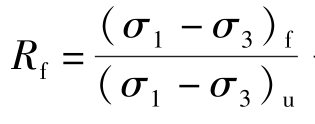——破坏比。

Duncan-Chang模型用于土体有限元分析时，能够反映土体变形的主要规律，但土体总变形中的塑性变形部分被当作了弹性变形处理；在有限元增量的计算中，Duncan-Chang模型反映了变形随应力路径变化的影响，但固结压力变化的区别没有体现，加荷和卸荷时泊松比υ的变化也没有体现。

（3）弹塑性本构模型

弹塑性本构模型反映材料的塑性变形。该模型可分为弹性阶段，此处为线性关系；屈服阶段，分为上屈服极限和下屈服极限；塑形流动阶段，流动阶段可长可短和材料有关。在弹塑性理论用于土体应力应变分析时，针对土体变形特点主要有两种塑性理论解释，分别是塑性形变理论和塑性增量理论，土的本构模型主要是建立在塑性增量理论基础上的。

在土的弹塑性模型形成的基础上，用于土体分析的弹塑性模型被分为两类：一类弹塑性模型的屈服函数、加工硬化定律等直接根据实验资料来确定，这类弹塑性模型的代表是Drucker-Prager（D.P）模型。Drucker-Prager模型屈服特性满足下列关系式：(www.xing528.com)

式中　σe——经过修正的等效应力；

σm——静水压力；

β——材料常数。

Drucker-Prager模型的应力应变对应关系为：

式中　σx，σy，σz，yz，zx，xy——6个应力分量；

——一点的平均应力；

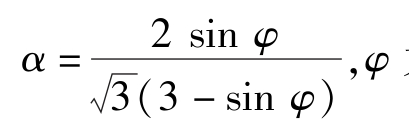为材料的内摩擦角；

J2——应力偏张量的第二不变量。

Drucker-Prager模型共有K，G，α，k共4个材料参数。K，G为弹性常数，可由E，ν换算出来。弹性参数α，k由Mohr-Coulomb准则的材料参数φ和c换算出来。

Drucker-Prager模型的最大优点是在考虑静水压力p对屈服和强度的影响时采用了简单方法，且在进行计算时模型参数较少，计算过程较为简单。但Drucker-Prager模型在计算时没有考虑材料在三轴方向强度不同状态下引起的材料屈服与破坏的影响。

在使用Drucker-Prager相关流动准则时，其弹塑性模量[D]ep为：

Drucker-Prager屈服面在主应力空间内为一圆锥形空间曲面，在π平面上为圆形，如图7.18所示。

图7.18　Drucker-Prager屈服面

可将Drucker-Prager材料的屈服准则写成以下修正形式：

材料参数β和σy被定义为：

式中　φ——内摩擦角；

c——黏滞力。

其中，当φ=0时，Drucker-Prager屈服准则将演变为VonMise屈服准则；当φ＞0时，在主应力空间上，Drucker-Prager屈服准则内切于Mohr-Coulomb准则屈服面的一个圆锥形空间曲面。同时，Drucker-Prager屈服准则避免了Mohr-Coulomb准则屈服面在角棱处引起的奇异点。

在采用DP塑性模型时需要输入3个参数量：黏滞力（剪切屈服应力）c、内摩擦角φ和剪涨角φf（该参数用于控制材料体积膨胀的程度）。如果φf=0，则不发生体积膨胀；如果φf=φ，则发生严重体积膨胀；如果φf＜φ，则发生较小体积膨胀。

另一类弹塑性模型是以能量公式为基础，推导其屈服函数，并选取合适的硬化规律，从而建立材料的应力-应变关系。这种模型一般也被称为临界状态本构模型；在20世纪50年代初，Drucker等认为土体存在一个由体积变化控制的帽子屈服面；Roscoe等基于临界状态的概念建立了模型框架，并认为存在一个状态边界面；Calladine则提出了塑性硬化理论，使土体的压缩和剪切特性在模型中统一起来。

剑桥模型是当前应用最广的弹塑性模型之一，Roscoe等以及Schofield等提出了最初的剑桥模型，后来Roscoe等提出了剑桥修正模型，20世纪70年代初，这些模型开始应用于数值分析中。剑桥模型适合于垃圾场防渗墙的应力-应变数值分析计算，但受到传统塑性理论的限制，且没有充分考虑剪切变形。修正的剑桥模型的状态边界面方程为：

令η=q′/p′，则修正后的剑桥模型其应力应变关系为：

以矩阵形式表示则为：

其屈服面方程为：

式中　μ——泊松比；

e——初始孔隙比；

λ——各向等压曲线斜率；

κ——回弹曲线斜率；

M——临界状态曲线斜率；

β——屈服面帽子曲度常量；

m，a——材料常数。

（4）其他力学本构模型

其他力学本构模型主要是由断裂力学、损伤力学等发展演变而来的。其中损伤模型主要包括单侧损伤、标量损伤、弹塑性损伤、各向异性损伤、断裂损伤及细观损伤模型等。基于断裂力学建立起来的模型主要有微裂纹面、多向定向裂纹及单向定向裂纹模型等。

对于大多数工程材料而言，在应力水平较低时，通常指小于比例极限，此时的应力-应变为呈线性关系。当大于这一值后，应力-应变呈非线性，然而这并不意味着是非弹性的。所谓的塑性是材料存在不能恢复的应变，当应力水平大于屈服强度时，继续加载的变形即为塑性变形部分。通常情况下，比例极限的值与屈服极限的值基本相近，因而在用ANSYS程序进行塑性分析时，认为这两个值为同一点，如图7.19所示。

图7.19　弹塑性应力-应变关系曲线

针对材料非线性问题的基本解法问题，通常采用线性解法的极限近似法，即通过一定的方法采用线性解答来逼近非线性的结果。常用的方法包括增量法、增量迭代法和迭代法。对于ANSYS非线性有限元的计算结果而言，需要注意的是，不能使用叠加原理，所计算得到的结果与荷载施加的路径相关，荷载施加的顺序不同会造成结构的响应也不同，结构的变形结果与受荷情况不是线性的。