康普顿效应实验规律-光学教程

观察康普顿效应的实验装置如图7-10所示。由X射线管发出一束单色X射线，经光阑D1、D2后被某种散射物质散射。散射光的波长和强度可以利用晶体衍射装置和探测器来测量。图7-11(a)表示，散射角θ不同时，散射X射线的强度随其波长而变化。图7-11(b)所示为在相同的散射角(θ=90°)条件下不同散射物质的康普顿散射。

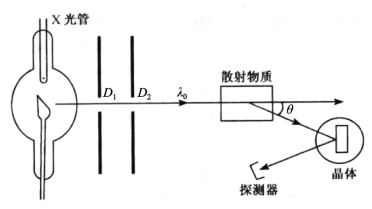
图7-10 康普顿效应实验装置图

图7-11 散射X射线的强度随其波长而变化的曲线

(注：横轴表示波长，纵轴表示散射X射线的强度)

由实验结果可知：

(1)散射光中除了和原波长λ0相同的谱线外，还有波长λ>λ0的谱线。

(2)波长的改变量Δλ=λ-λ0与原入射波长λ0和散射物无关。而只与散射方向有关。如果用θ表示原射线方向和散射线方向间的夹角，则波长的改变量Δλ与散射角θ角之间的关系可表示为

式中，λc=2.426×10-12m，是由实验测定的常数。

(3)散射光中波长为λ0的谱线强度随θ角的增加而减小。若用不同元素作为散射物质，则波长为λ0的谱线强度又随散射物质原子序数的增加而增加；相反散射光中波长为λ的谱线强度随θ角增加而增加，并且随散射物质原子序数的增加而减弱。

从经典波动理论来看，散射光是物质中的电子在入射光波电场的作用下，作受迫振动时辐射的次波，电子作受迫振动的频率等于入射光的频率，因此散射波长应等于入射光的波长。可见经典理论不能解释X射线经物质散射后波长发生变化的现象。

康普顿利用光子理论成功地解释了散射光中波长的改变。他把X射线被散射物质所散射，看成是入射的X射线的光子与散射物质中的自由电子作弹性碰撞的结果。它认为光子作为一种微粒，不仅具有能量而且具有动量。由于X射线的波长极短，光子的能量和动量要比散射物质中一些电子原来的动能和动量大得多(例如，轻的原子中的外层电子和原子最外层电子受原子核的束缚比较微弱。结合能为10～100eV，而波长λ=0.7nm的Ka线，其能量约为2×104eV)。故前者可忽略不计，即可假定电子在碰撞前是静止的，自由的光子与自由静止电子碰撞后沿某一方向散射，就构成沿某方向的散射光。碰撞时入射光子把一部分能量交给电子，所以碰撞后的散射光子具有较小的能量，这意味着散射X射线的频率比入射X射线小，或波长变大，这就解释了康普顿散射的基本事实。

因为X射线的光子能量比较大，与散射物质中的自由电子碰撞后，可使电子获得很大的速度，所以在利用光子理论来导出康普顿散射所遵从的规律时，最好采用狭义相对论的一些结论。在这里简单介绍。狭义相对论指出粒子的运动质量(简称质量)m随其速度v而变，其关系为

m0为v=0时粒子的质量，称为静止质量，c为真空中的光速，因为光子的速度为c。所以光子的静止质量m0只能为零。否则由式(7-18)会得到光子质量无穷大的结论。相对论还表明，粒子质量与能量有着紧密的联系，两者间的关系可用著名的质能关系来表示：

对静止粒子，其能量为m0c2。由式(7-19)可知，光子的质量为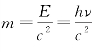。因为光子以速度v运动，所以光子的动量为

式中，ν为光子的频率。(www.xing528.com)

现在利用以上结论来定量分析入射X射线的一个光子与处于静止状态的一个自由电子的弹性碰撞过程(图7-12)。在此过程中能量和动量守恒的方程为

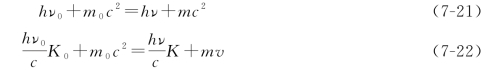
式中，K0、K分别表示光子在入射方向和散射方向的单位矢量。ν0和ν分别是碰撞前后光的频率，m为电子运动质量，v0为碰撞后电子的反冲速度。由图7-12可得

将式(7-21)移项写成

把上式平方后减去式(7-23)，得

根据关系式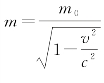，有，上式可改写为

将频率ν和ν0用相应的波长λ和λ0表示，并令Δν=ν-ν0，Δλ=λ-λ0，从上式可以得到

因为h、c和电子静止质量m0都已知，所以可算出

λc是一个具有长度量纲的常数，称为康普顿波长。由计算结果可以看到它与实验数据相符合。

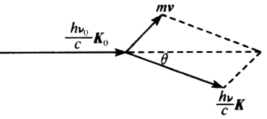
图7-12 弹性碰撞

那么，为什么散射光中存在与入射光波长λc相同的谱线呢?这是因为在上面的计算中，假定了电子是自由的静止电子。实际并不尽然，特别是重原子中内层电子被束缚得较紧。光子与这种电子碰撞时，实际上是在和一个质量很大的原子交换动量和能量，从而光子的散射只改变方向，能量几乎不变。这就是散射光中总存在原波长λc这条谱线的缘故。由于原子中内层电子数目随原子序数的增加而增加，所以波长为λc的谱线强度也就随之增强，而波长λ的谱线则随之减弱。

在以上的讨论中，假定电子在碰前是静止的，而实际上电子处于各种可能的运动状态，碰前动量并不等于0。这导致散射光中包括各种可能的波长，即散射光强度按波长的分布实际上是出现两个峰值的连续分布(图7-11)。

康普顿效应不仅证实了光的微粒性，也证实了微观粒子的相互作用在一定条件下也满足能量守恒和动量守恒定律。