光在球面上的折射原理

现在研究光在球面上的折射情况，自物点P(图4-12)发出的任一条光线PA，经球面折射后，折射光与主轴的交点为P'，在三角形PAC和P'AC中根据正弦定理有

由图可知，PC=(-s)+r=r-s，CP'=s'-r因而上两式写为

应用折射定理nsin(-i)=n'sin(-r)，则上两式合并为

或

由上式可知，当物点P的位置一定时，折射光线与主轴的交点位置P'将随入射光线与主轴的夹角u而变(式中u'随u而变)，因此单心光束经球面折射后，折射光束不再是单心光束。可简单说明如下：由物点P发出的沿主轴方向入射球面的光线PO，折射光线是OP'。由于不同的入射光线经球面折射后与主轴的交点是不同的，即折射光线不相交于一点，因此折射光束不是单心光束。

但是，如果角度很小，sinu≈tgu≈u，由图4-12可知

将其代入式(4-9)有

上式表明，物点P一定时，折射光束将会聚于一点，显然，只有光在sinu≈u区域内折射，光束才能保持单心性，满足这样条件的光线称为近轴光线，研究近轴区域内成像规律的光学称近轴光学或高斯光学。

公式(4-10)是表示在近轴区域内物与像之间关系的物像公式，可以看出，若物点在P点，则其像点将位于P'点，物点与像点的这种对应关系称为共轭，相应的点称为共轭点，相应的光线称为共轭光线。

对于不同的球面(有不同的n，n'或r)来说，给定的物点将有不同的像点，式(4-10)中右端的物理量反映了球面的光学特征，称此物理量为光焦度，令

式(4-10)中，折射率n和n'分别是物空间和像空间的折射率，所谓物空间是指入射光线在其间行进的空间；而折射光线在其间行进的空间称像空间。

当物点F位于无限远处(s=-∞)时，即当平行于主轴的平行光在球面上折射时，其共轭像点F'的位置为

(www.xing528.com)

共轭点F'称为像方焦点(或第二焦点)，像方焦点F'到球面顶点的距离f'称为像方焦距(或第二焦距)；当像点位于无限远(s'=∞)时，其对应的共轭物点F称为物方焦点(或第一焦点)，F到球面顶点的距离f称为物方焦距(或第一焦距)，f由下式决定

由式(4-12)、式(4-13)可得

上式说明物方焦距与像方焦距各在球面顶点的两侧并且大小不等(因n和n'不可能相等)。

将物方焦距和像方焦距引入近轴区域内光经球面折射时的物像公式中，用光焦度ϕ=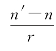除以式(4-10)有

将式(4-12)和式(4-13)代入可得

此式称为高斯公式。

如果我们在求物点和像点的位置时不从球面顶点算起，而分别从物方焦点F和像方焦点F'算起，则可把高斯公式写成牛顿公式的形式，由图4-13可知

-s=-x-f， s'=f'+x'

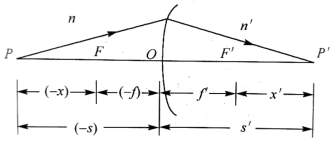
图4-13 高斯公式和牛顿公式物像距的关系

将其代入高斯公式有

简化后，即得牛顿公式

物像公式(4-10)、高斯公式(4-15)和牛顿公式(4-16)均反映了近轴区域内光经球面折射成像的规律，只不过形式不同而已，三者是等价的。