光在平面上的折射-成果直接输出

图4-10中，OO'表示两种介质n1和n2(假设n1>n2)的分界平面，PA1和PA2是自物点P发出的两条光线，经界面折射后折射光束是发散的，这两条折射光线的反向延长线相交于P'点，相交PN于P1和P2点。现在研究折射光束是否是单心光束，对此，不能简单地通过两条光束判定，必须考虑折射光束中光线的空间分布情况，这可以将图4-10绕ON轴转过一个很小的角度，即可得到由PA1A2经转动面构成的很小范围内的空间单心光束，以及这部分光束经折射后折射光束的空间分布情况。此时，折射光束中所有光线的反向延长线的交点都位于线段P1P2上，同时，当图以ON为轴转过一个很小的角度时P'点将描出一段很短的弧线，可以认为是垂直于图面的一小段直线。由此可见，折射光束中所有光线并不相交于一点，而是相交于两条相互垂直的线段上，一条是由P'点描出的线段，另一条是P1P2线段，这样的两条线段称为像线。其中由P'点描出的垂直于图面的像线称为子午像线；位于图面内的线段P1P2称为弧矢像线。

图4-10 光在平面上的折射

单心光束经平面折射后，波阵面的形状发生了变化，不再是原来的球面，而变成非球面的高次曲面，图4-11是一个任意曲面的一部分。根据微分几何知识，在曲面上的任一点O，通过此点对曲面作的所有截线中，曲率半径最大的截线GOD和曲率半径最小的截线FOH是相互垂直的，设前者的曲率中心在C2，后者的曲率中心在C1，则由点G、O和D所引的法线相交于曲率中心C2，自F、O和H三点所引的法线相交于曲率中心C1。现作出截线AFE和BHC接近和平行于截线GOD，它们应有相同的曲率半径，因此由A、F、E、B、H、C诸点所引的法线必相交于通过C2点的直线bb'上。同样，对于截线FOH于它接近和平行的截线AGB和EDC上各点所应的法线，应相交于过C1点的直线aa'上，直线aa'和bb'相互垂直，因而，相应于任意曲面的光线，其交点都在相互垂直的两个线段aa'和bb'上，都相交于子午像线和弧矢像线，这样的光束就是上节介绍的像散光束。(www.xing528.com)

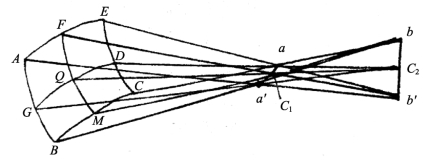
图4-11 光在球面上的折射

可以证明，只有当P点发出的光束几乎垂直入射界面时，图4-10中的P'、P1和P2才能重合于一点，即这时的折射光束几乎是单心光束，这正是在靠近水平面的法线方向观看水中物体时，像很清晰的道理，而沿倾斜的角度观看时，清晰的像就散乱了。