费马原理是由费马于17世纪中期首次提出：光由一点传播到另一点处，光沿光程取最小值的路径传播。后来发现，光线在曲面上反射或折射时并不沿光程取最小值的路径传播，经修改，现将费马原理表述如下：光由一点传播到另一点，光沿光程取极值的路径传播；取极值的含义是，光程可取最小值，最大值或常数，其数学表达式如下
光在均匀介质和非均匀介质(即介质各点处折射率不同，如热天的大气)中的传播均遵守费马原理，它是光线传播普遍遵守的规律，下面用费马原理推导反射定理和折射定理。
图4-1中，由A点发出的光线经平面镜MM'反射后通过C点，其中ABC这条光线是遵守反射定律的，ADC是任意一条光线，由于从A点经平面镜反射通过C点的所有路径都在同一介质中，因此为求光程取极小值的路径只需考虑长度取极小值的路径即可，为此，过A点作平面镜的垂线交平面镜于E，并在其延长线上取一点A'，使AE=A'E。根据几何定律可知A'BC是一直线。显然在三角形A'CD中有
即
因此根据费马定律，从A点发出的光线只有遵从反射定律的光线才能被平面镜反射到达C点。
图4-1 利用费马原理证明反射定律
图4-2中，自给定的A点发出的光线AB在两种介质的界面OO'上发生折射，折射光通过C点。光线沿ABC路径传播的光程为
式中，h1和h2分别是从两给定点A和C到界面OO'的距离，是常数。根据费马原理，从给定A点到C点的所有路径中，光只沿光程取极值的那条路径传播，即
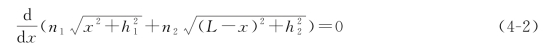(www.xing528.com)
具体写出来为
从图可以看出
由此式(4-3)可以写为
这就是折射定律。
在第二章第四节中曾指出，从一发光点P所发出的各条光线经凸透镜折射后到达P'点的光程均相等，即物象之间的等光程原理，这里用费马原理作一个定性的证明。图4-3中，从P点到P'点的路径中显然直线PP'的路径最短，而折线PTP'的路径最长，但是从光程的角度来看，光在直线传播时，其在空气中的光程最小，但在透镜中的光程最大；光沿折线PTP'传播时，光在空气中的光程最大，而在透镜中的光程最小。根据费马原理，从P点发出的光线能通过直线PP'以及折射PTP'和PQRP'到达P'点，那么它们的光程都应取极值，显然，它们的光程必然相等。
图4-2 利用费马原理证明折射定律
图4-3 等光程原理
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
