光栅方程原理及计算结果

单色光经光栅衍射产生的各级主最大，称该单色光的光谱线。如前所述相邻缝发出的相干光束的光程差为dsinθ，当相邻光波位相差满足Δφ=2jπ(j=±0，±1，±2，…)时产生主最大，故各级光谱线的位置满足

上式称为光栅方程，其中j称光谱线的级数。在衍射角θ满足光栅方程的方向上将出现光谱线，光栅方程是决定各级谱线位置的公式。式(2-30)适用于平行光波垂直入射光栅的情况。如果平行光波与光栅平面的法线方向成一夹角φ入射光栅时，多缝干涉中的相邻光波在入射前已有dsinφ的光程差，故光栅方程写为如下形式

当入射光与衍射光在法线同一侧时，如图2-21(a)所示，上式左边括号内取加号，在法线异侧时，如图2-21(b)所示，取减号。

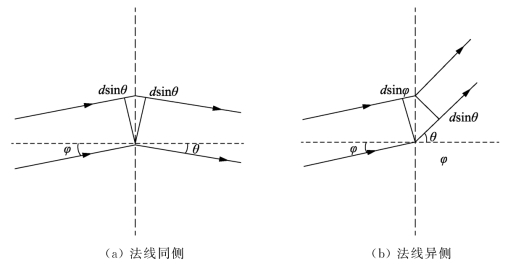
图2-21 平行光斜入射光栅

通常，在满足光栅方程的衍射角θ方向上将有与主最大对应的亮条纹出现，但由于光栅的光强是由干涉因子和衍射因子这两个因素的乘积决定的，在满足光栅方程的衍射角方向上，单缝衍射在该方向上的光强如果恰好为0，那么该方向上的合成光强必为0，即发现缺级现象。所以在发生缺级时，衍射角必同时满足下列两式

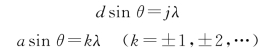
式中，整数k是夫琅和费单缝衍射光强最小的级数，将上两式相除消去θ，即得缺级的光谱线级数为

例如光栅常数是缝宽的三倍时，即则第3级、第6级、第9级……谱线将消失，图2-20(c)中就是这种情况。

各级光谱线都有一定的宽度，谱线的宽度是由主最大两侧的暗线间的距离确定的，谱线的宽窄反映了光栅性能的优劣，从某一级主最大的中心到最靠近该主最大的最小值之间的角距离，就是该级谱线的半角宽度Δθ，设第j级谱线的衍射角为θ，则最靠近该谱线的最小值对应的衍射角为θ+Δθ，有

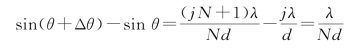(www.xing528.com)

通常Δθ很小，故上式可写为

于是

由此可见，光栅的缝数N愈大，谱线愈细。

例2-4：用波长为5000Å的单色光照射缝宽为0.1×10-3cm，相邻缝间距为0.2×10-3cm的衍射光栅，问能观察到几条谱线?

解：根据光栅方程(2-30)

依题意d=a+b=0.1×10-3+0.2×10-3=0.3×10-3cm，能观察到的最高级数为

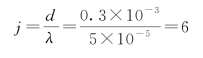
考虑到缺级，所缺级数为

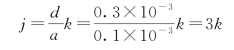
即第3级、第6级缺级，所以能观察到的谱线为0，±1，±2，±4，±5共计9条谱线。