菲涅耳半波带法及应用

如图2-6所示，O为一单色点光源，S是O点发出的球面波在某一时刻的部分波面，B0为空间任一点P与O点连线的交点。为求波面S在P点处产生的振动，以P点为中心，将波面化分成许多环形带，使两个相邻环形带的边缘到P点的距离相差均为半个波长，即

这样，每两个相邻环形带中对应部分发出的次波到P点的光程差均为，位相差为π，因此相邻环形带对应部分发出的次波在P点的振动方向相反，这种环形带称菲涅耳半波带。

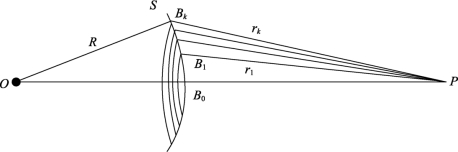
图2-6 菲涅耳半波带

由于相邻带发出的次波在P点的振动相反，设其中一个带发出的次波在P点的振动振幅为正，则相邻带发出的次波在P点的振动振幅为负，于是使得波面S在P点产生的振动振幅为

式中，E10，E20，E30，…，Ek0分别是第一个带到第k个带在P点处产生振动的振幅，下面证明各带的面积相等。

由图2-7可知第k个环形带边缘半径为

式中，h为O'B0间的距离，由上式可得

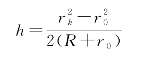
由于

故

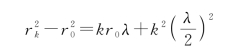
通常λ≪r0，上式中二阶小项略去，近似有

将上式代入h表达式，得

根据球冠面积公式，可求得包含k个环形带的波面的面积为

则第k个环形带的面积为

(www.xing528.com)

由上式可知，第k个带的面积与其序号k无关，即各带面积相等。

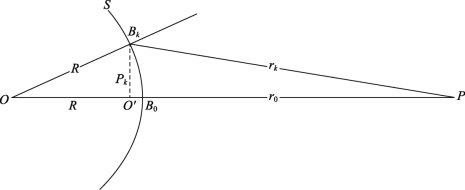
图2-7 菲涅耳半波带面积的计算

根据惠更斯-菲涅耳原理，任何一个环形带在P点产生的振动振幅，与带的面积ΔSk，带到P点的距离rk及倾角θ有关。图2-7可看出，由于各带面积相等，随着环形带序号的增加，rk变大，θk也变大，因此各带在P点产生的振动振幅，随着序号的增加而单调地减小，即

各带在P点产生的振动振幅，近似有如下关系

如果波面只包含k个环形带，则当k为奇数时，式(2-4)写为

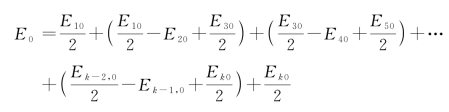
当k为偶数时

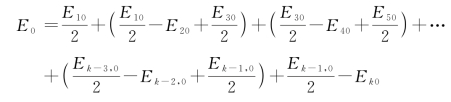
将关系式(2-10)代入上两式，便得k为奇数时

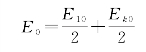
当k为偶数时

如果环形带数目很多，Ek-1，0与Ek0相差很小，当k为偶数时近似有

合起来写有

式中，正负号的取法，随波面所包含的半波带奇偶数而定，半波带数为奇数时取正，为偶数时取负。

菲涅耳半波带法，把菲涅耳衍射积分公式化为有限项的求和，避免了复杂的数学计算，可以对一些衍射现象做出较好的解释。