惠更斯-菲涅耳原理解读|光学教程

为说明波在空间的传播机理，惠更斯提出了次波假设来解释波的传播现象，称为惠更斯原理：任何时刻波面上的每一点，都可看作是产生球面次波的波源，在以后任意一时刻的新的波面就是这些次波的包络面。

图2-2(a)、(b)中S为t时刻球面波和平面波的波面，设波在各向同性和均匀介质中传播，波的传播速度为v，为求下一时刻t+Δt时的波面，根据惠更斯原理可以把S上的每一点都看作是次波的波源，以波面上各点为中心，画出半径为vΔt的球面，再画出与这些球面相切的面，即包络面，便得到下一时刻t+Δt的波面S1，波面的法线就是波的传播方向。由此可知，球面波和平面波在下一时刻的波面仍是球面波和平面波。

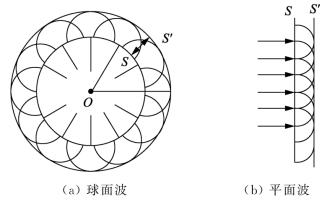
图2-2 利用惠更斯原理求球面波和平面波的波面

图2-3中当点光源O发出的球面波传播到带有开孔的不透明屏D时，由于开孔的限制，只有ASB部分波面能够通过，根据惠更斯原理画出光通过开孔后的波面S'，由图可知，边缘部分的光将不再按原来的方向传播，可以预料将有光进入投影区外。

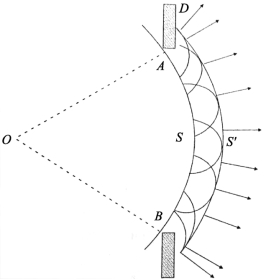
图2-3 利用惠更斯原理解释光偏离直线传播现象

应用惠更斯原理可以广泛地确定光在空间中的传播方向，由于惠更斯原理仅阐明了不同时刻波面之间的几何关系，而没有涉及波动的时空周期性，因此不能确定光波传播到各点时的振幅和位相这些问题，不能解释衍射图样中光强的分布问题。菲涅耳在惠更斯原理的基础上，根据光的干涉原理提出各次波源发出的球面次波在空间相干叠加，形成了惠更斯-菲涅耳原理：①如图2-4所示，波面S在空间任意一点P处产生的振动等于各微元面dS，在P点处振动的总和。②微元面dS发出的球面次波在P点的振动振幅与面积元dS成正比，与dS到P点的距离r成反比，且与倾角θ有关，随θ角的增大而减小。③波面上各微元面的初位相均相同(可令Δφ0=0)。

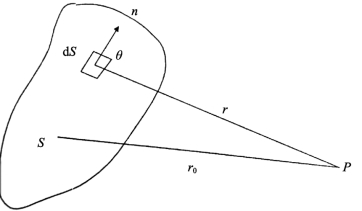
图2-4 惠更斯-菲涅耳原理

任意一微元面在P点的振动位相取决于该微元面到P点的光程差nr。于是微元面dS在P点产生的振动可表示如下：

(www.xing528.com)

或

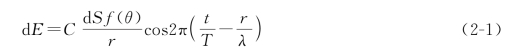
式中，C是比例常数，f(θ)是随θ角增大而减小的函数，称为倾斜因子。将各微元面在P点处的振动加起来即得波面S在P点处的总振动

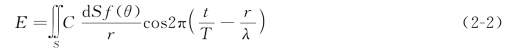
上式称为菲涅耳衍射积分公式。

惠更斯-菲涅耳原理可以完满地解释许多衍射现象，但它是建立在假设基础上的，缺乏严格的数学推论，1882年基尔霍夫由格林定理出发，从数学上做了严密推导，得到了基尔霍夫衍射积分公式

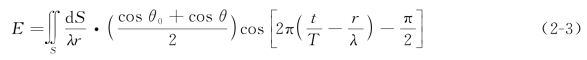
基尔霍夫公式给出了倾斜因子的具体表达式，解决了倒退波问题，给出了P点的准确位相及比例常数C的值。在大多数情况下，我们只考虑衍射花样的强度分布，的位相差异对衍射花样没有影响，倾斜因子的具体形式对计算结果影响不大。因此，惠更斯-菲涅耳原理是处理衍射问题的理论基础。

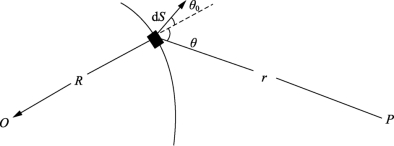
图2-5 基尔霍夫衍射积分公式中的各物理量