光的衍射现象及菲涅耳衍射的发现

光在透明介质中沿直线传播是我们从日常生活中得到的经验，也是几何光学的基础，但若光在传播途中遇到尺度很小的障碍物，如狭缝、小孔、细丝等时，则可观察到光偏离直线传播的现象，这种现象称为光的衍射。

如图2-1所示，S是点光源，D为带有圆孔的不透明屏，圆孔半径可以调节，P为接收屏。当圆孔半径较大时，屏上呈现一个均匀照明有清晰边界的圆形光斑，它是入射光束沿直线投射的结果。随着圆孔半径减小，光斑也相应地变小，当圆孔半径减小到一定程度时，光斑变成一组明暗相间的同心圆环，边缘失去明显的界线，随着半径的变化，衍射花样的中心是亮暗交替变化的。如果用圆屏代替上述圆孔，也可观察到明暗相间的同心圆环，但与圆孔不同的是衍射花样的中心始终是一亮点。

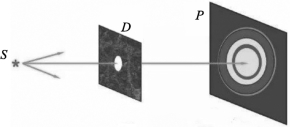
图2-1 光的衍射现象(www.xing528.com)

1818年，当菲涅耳关于衍射的论文提交法国科学院时，泊松根据菲涅耳的衍射理论推导出圆屏衍射花样中心是一亮点这一似乎荒谬的与人们的经验完全相反的结论，作为推翻菲涅耳理论的证据而提了出来。不久，阿拉果在实验中发现了这一事实，这一事实的发现不仅证实了菲涅耳理论的正确性，也确立了光的波动本性。

干涉和衍射是波动所特有的属性，光的衍射现象是光的波动特征的表现。机械波、无线电波等在传播途中遇到障碍物时，也将发生衍射现象，例如墙外的人能够听到院内的讲话声音，电台和接收机中间隔着大山，也能接收到无线电波等。但在日常生活中光的衍射现象却不易观察到，这是因为光的波长很短，而通常障碍物的尺寸较大，且普通光源是非相干光源。在实验室中采用激光作为光源，就很容易观察到光的衍射现象。

在研究光的衍射现象时，通常按光源和观察点到障碍物的距离的不同把衍射分为两类。一类是障碍物到光源和观察点的距离都是有限的，或二者之一为有限远，这类衍射称菲涅耳衍射。另一类是光源和观察点到障碍物的距离均为无穷远，这类衍射称夫琅和费衍射。