在前面讨论中我们没有涉及光源本身的大小,实际光源总是有一定大小的,这就给干涉条纹的可见度带来一定的影响。在杨氏双缝干涉实验中,当光源缝宽较小时,可以在屏幕上观察到较清晰的干涉条纹,随着缝宽增加,干涉条纹变得模糊,干涉条纹可见度降低,当缝宽增大到一定程度时,干涉条纹的可见度降为零,干涉条纹将消失。
光源上不同部分发出的光是不相干的,各部分发出的光经干涉装置后在屏幕上形成各自的干涉花样,且相互错开,这些干涉花样的非相干叠加造成干涉条纹的可见度降低甚至为零。空间相干性就是研究在多大的尺度范围内普通光源发出的光在空间相遇时能形成干涉现象的问题。
如图1-12所示,在杨氏双缝实验中,设单缝宽度为a,把它看成是由许多线光源构成的,单缝中心处线光源S发出的光到双缝S1、S2的光程相等,即光程差为零,其在屏上产生的干涉图样的零级亮条纹位于中心P0处。由位于单缝边缘处线光源S'发出的光波到达S1、S2时,由于光程不等,有光程差δ=R1-R2,因此,由光源S'发出的光波在屏上形成的干涉图样的零级亮条纹(光程差为零处)向下移动了一段位移δy,位于P'0处,P'0的位置由下式决定。
![]()
或
![]()
由图1-12可得
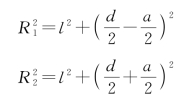
两式相减得
![]()
因a≪l,d≪l,有
![]()
故
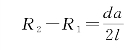
式(1-34)中r2-r1可由第四节杨氏双缝实验的光程差公式(1-24)确定,故
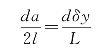
有
 (https://www.xing528.com)
(https://www.xing528.com)
由此可知,单缝边缘处线光源S'产生的干涉条纹的位移δy在单缝到双缝的距离l和双缝至屏的距离L一定时,与单缝的宽度a成正比。
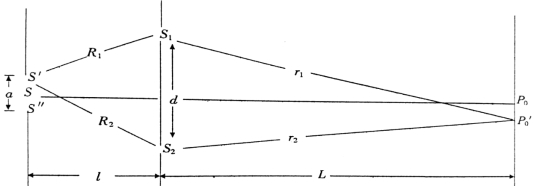
图1-12 空间相干光程差计算图
由第四节的讨论可知,杨氏双缝干涉图样中相邻明条纹和暗条纹的间距是相等的,间距为
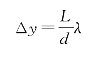
即各级亮条纹和暗条纹的宽度为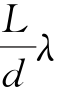 ,当S'产生的干涉零级与S产生的第一级暗条纹重合时,整个屏上的干涉花样的可见度为零,干涉条纹完全消失,这时光源宽度的临界值为
,当S'产生的干涉零级与S产生的第一级暗条纹重合时,整个屏上的干涉花样的可见度为零,干涉条纹完全消失,这时光源宽度的临界值为
![]()
显然,随着光源宽度的增大,干涉条纹的可见度减小,当增大到其临界值时,干涉条纹的可见度变为零。
例1-3:在杨氏双缝实验中,双缝间距为0.5mm,光源距双缝20cm,试求:(1)若光源波长λ=5000Å,谱线宽度Δλ=100Å,屏上能看到的最高干涉级。(2)若光源有一定的宽度,屏上干涉条纹消失时,其临界宽度是多少?
解:(1)当波长为![]() 的第j+1级亮条纹与波长为
的第j+1级亮条纹与波长为![]() 的第j级亮条纹重合时,即当
的第j级亮条纹重合时,即当
![]()
各种成分的波长的亮条纹连成一片,可见度降为零,因λ>>Δλ有
![]()
依题意,λ=5000Å,Δλ=100Å
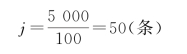
(2)光源宽度的临界值为
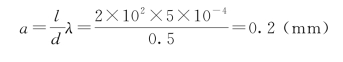
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




