光学教程：杨氏双缝实验装置及干涉图样

1801年，英国物理学家托马斯·杨，利用双缝将通过一准直缝后的单色光的波面进行分割，观察到了光的干涉现象，这个实验构思巧妙，实验装置极为简单，在确立光的波动理论上杨氏实验具有决定性的意义。

图1-5(a)是杨氏双缝实验装置示意图，在普通单色光源前放一开有小孔S的屏，在通过小孔S的光波行进途中放置一块开有两个小孔S1和S2的屏，后来发现以狭缝代替小孔可获得更加明亮的干涉图样。实际实验中是用狭缝代替小孔。光波通过S1和S2后继续传播，在任何时刻，由点光源S发出的球面波的同一波面，被S1和S2分割为两部分，因此透过S1和S2的光波是满足相干条件的相干光，在叠加区域可用光屏和目镜观察到明暗相间的干涉条纹，如图1-5(b)所示。

图1-5 杨氏双缝实验图

设两平行狭缝S1和S2之间的距离为d，缝到光屏的距离为L，P是屏上任一点，距P0的距离为y，S1和S2到P点的距离分别为r1和r2，由图1-6可知，由S1和S2发出的光波在P点的光程差δ=r1-r2。在直角三角形PS1S'1和PS2S'2中有

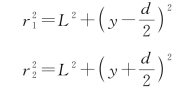
上两式相减得

在杨氏双缝实验中有L≫d，r2+r1≈2L，由上式得

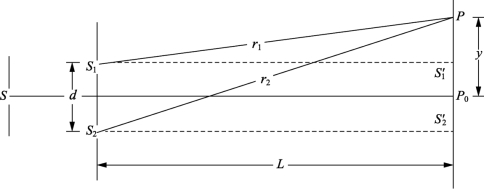
图1-6 干涉条纹计算图

屏上呈现亮条纹的区域，应满足δ=jλ(j=0，±1，±2，…)，其到P0的距离y由式(1-24)可得

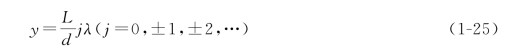
式中，j称为干涉级，j=0对应的条纹称零级亮条纹或中央亮条纹，j=1对应的亮条纹称第一级亮条纹，其余类推。

呈现暗条纹的区域到P0的距离为

同样，j=1，2，…对应的暗条纹，分别称第一级暗条纹、第二级暗条纹……(www.xing528.com)

相邻亮条纹(或暗条纹)的间距为

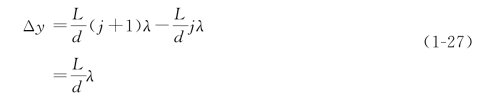
由式(1-27)可知，杨氏双缝实验的干涉图样相邻亮条纹和暗条纹的间距是相等的。如果实验中光源采用包含各种波长的光(白光)，除零级亮条纹外，其余各级亮条纹是有颜色的。从两狭缝S1和S2发出的光波振幅相等。屏上任一点处的光强度根据式(1-18)为

可得双缝干涉光强分布曲线为图1-7所示。

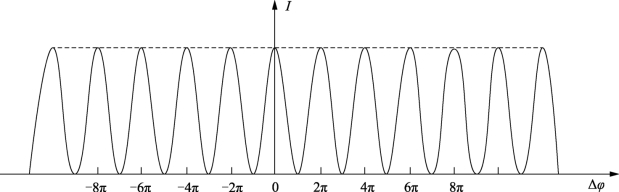
图1-7 杨氏双缝实验光强分布曲线

例1-1：在杨氏双缝实验装置中，双缝间距为0.5mm，缝到光屏的距离为1m，若在S1后插入一块折射率n=1.5的玻璃片，观察到零级条纹移动了5mm，试求插入的玻璃片厚度。

解：设S1后插入玻璃片厚度为x，则S1，S2至P点的光程差为

根据式(1-24)，可知

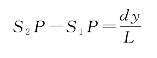
故

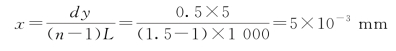
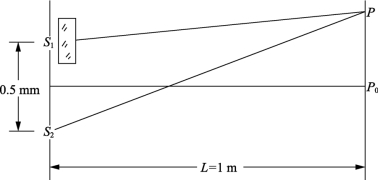
例1-1图