线性方程组αs的基础解系及性质

线性方程组的克拉默（Cramer）法则 齐次线性方程组有非零解的充分必要条件 非齐次线性方程组有解的充分必要条件 线性方程组解的性质和解的结构 齐次线性方程组的基础解系和通解 非齐次线性方程组的通解

1．会用克拉默法则．

2．理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件．

3．理解齐次线性方程组的基础解系及通解的概念，掌握齐次线性方程组的基础解系和通解的求法．

4．理解非齐次线性方程组的解的结构及通解的概念．

5．会用初等行变换求解线性方程组．

1.齐次线性方程组与其基础解系（考点16）

齐次线性方程组必有解，但什么时候有非零解是我们更关心的，在有非零解（无穷多解）时如何求出这些解？这就需要找到无穷多解的极大无关组了，也就是我们所说的基础解系．

2.非齐次线性方程组（考点17）

首先，要清楚非齐次线性方程组解的判定，其次，要通过练习熟练求解各类方程组，如参数型、抽象型、矩阵方程型等．

3.公共解与同解（考点18）

公共解与同解的考法和做法详见后面考点18．

考点16 齐次线性方程组与其基础解系

1．齐次线性方程组的表示

齐次线性方程组

2．非零解的判定（必有解）

（1）Am×n x＝0只有零解⇔r （Am×n）＝n（未知数个数、A的列数）；

（2）Am×n x＝0有非零解⇔r （Am×n）＜n（未知数个数、A的列数）．

3．解的性质

若ξ1，ξ2是Ax＝0的解，则kξ1，k1ξ1＋k2ξ2仍是Ax＝0的解．

若Am×n x＝0有非零解（即有无穷多解），则线性无关的解有n－r（A）个，且它们能表示任一解．

4．基础解系

称α1，α2，…，αs是齐次线性方程组Am×n x＝0的基础解系，当且仅当

（1）α1，α2，…，αs是Ax＝0的解；

（2）α1，α2，…，αs线性无关；

（3）α1，α2，…，αs可以表示Ax＝0的任一解或n－r（A）＝s．

Ax＝0的通解为k1α1＋k2α2＋…＋ksαs，其中k1，k2，…，ks为任意常数．

如设A是4阶矩阵，A*为A的伴随矩阵．若线性方程组Ax＝0的基础解系中只有2个向量，则r（A*）＝（ ）．

（A）0 （B）1 （C）2 （D）3

答案（A）

解析 由于方程组Ax＝0的基础解系中只有2个向量，则n－r（A）＝4－r（A）＝2，得r（A）＝2＜3，故r（A*）＝0．因此选（A）．

5．基础解系的求法

求基础解系时，可对A作初等行变换化为阶梯形矩阵，通常称每个非零行中第一个非零系数所代表的未知数是主元（共有r（A）个主元），那么剩余的其他未知数就是自由未知量（共有n－r（A）个），当然也可在加减消元后找出秩为r（A）的行列式，那么其他各列的未知数就是自由未知量．对自由未知量按阶梯形赋值后，再代入求解即可得到基础解系．

例如，若某齐次线性方程组Ax＝0经消元，化为

则n－r（A）＝5－3＝2，说明基础解系由2个向量组成．此时x1，x3，x4是主元，x2，x5是自由未知量，因而可对自由未知量赋值为［x2，x5］T＝［1，0］T及［0，2］T．

再由下往上代入求解，得η1＝［1，1，0，0，0］T，η2＝［－3，0，6，3，2］T，即为Ax＝0的基础解系．因为

所以也可取x1，x4为自由未知量，然后赋值求解．

因为［1，0］T，［0，2］T线性无关，延伸后η1，η2必线性无关，在η2中令x5＝2，是考虑x4的系数是2，为回避分数运算而设定的，通常令x5＝1．读者要理解基础解系的概念，能正确、迅速地求解．

类型一：解方程

知r（A）＝3．由于n－r（A）＝5－3＝2，故方程组Ax＝0的基础解系由两个线性无关解向量组成，其中x3，x5是自由未知量，分别取x3＝1，x5＝0与x3＝0，x5＝1，回代（由下往上代）方程组

得基础解系

故方程组的通解是k1α1＋k2α2，其中k1，k2是任意常数．

基础解系不唯一．实际上，为了回避x2的分数，可以取x3＝0，x5＝6．

设齐次线性方程组

试问a取何值时，该方程组有非零解，并求出其通解．

解 对方程组的系数矩阵A作初等行变换，有

当a＝0时，r（A）＝1＜4，故方程组有非零解，其同解方程组为

x1＋x2＋x3＋x4＝0，

由此得基础解系为

η1＝［－1，1，0，0］T，η2＝［－1，0，1，0］T，η3＝［－1，0，0，1］T，

于是所求方程组的通解为

x＝k1η1＋k2η2＋k3η3，其中k1，k2，k3为任意常数；

当a≠0时，

可知当a＝－10时，r（A）＝3＜4，故方程组也有非零解，其同解方程组为

由此得基础解系为

η＝［1，2，3，4］T，

于是所求方程组的通解为

x＝kη，其中k为任意常数．

当a＝－10时，系数矩阵化成了不好进一步化成行阶梯形矩阵，但此时对于找方程组的解已经够用了，读者不必过分地拘泥于行阶梯形矩阵．当然，大多数情况下都化成行阶梯形矩阵．

设n阶矩阵A的各行元素之和均为零，且A的秩为n－1，则线性方程组Ax＝0的通解为__________．

答案 k［1，1，…，1］T，其中k为任意常数

解析 因为Ax＝0的基础解系含向量的个数为n－r（A）＝n－（n－1）＝1，故Ax＝0的任一非零解都可以作为它的基础解系．由已知ξ＝［1，1，…，1］T是Ax＝0的一个非零解，从而ξ可作为Ax＝0的基础解系，故得通解为x＝k［1，1，…，1］T，其中k为任意常数．

类型二：AB＝O

设Am×n Bn×s＝O．

证明 ：（1）B的每一列都是齐次线性方程组Ax＝0的解；

（2）r（A）＋r（B）≤n．

证明 （1）对B及O按列分块，有A［α1，α2，…，αs］＝［0，0，…，0］，于是Aα1＝0，Aα2＝0，…，Aαs＝0．故B的每一列（即αi）都是方程组Ax＝0的解．

（2）当Ax＝0有无穷多解时，其线性无关的解有n－r（A）个，又B的每一列（有限个）都是Ax＝0的解，但这些解中只有r（B）个是线性无关的，于是r（B）≤n－r（A），故r（A）＋r（B）≤n．

设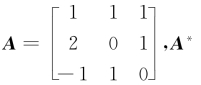是A的伴随矩阵，则A*x＝0的通解是__________．

答案k1［1，2，－1］T＋k2［1，0，1］T，其中k1，k2为任意常数

解析 由于｜A｜＝0，秩r（A）＝2，知r（A*）＝1，那么n－r（A*）＝3－1＝2，从而A*x＝0的通解形式为k1η1＋k2η2．

又A*A＝｜A｜E＝O，故A的列向量均是A*x＝0的解，所以A*x＝0的通解为k1［1，2，－1］T＋k2［1，0，1］T，其中k1，k2为任意常数．（答案不唯一）

已知3阶矩阵A的第一行是［a，b，c］，a，b，c不全为零，矩阵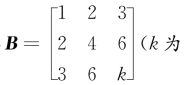

常数），且AB＝O，求线性方程组Ax＝0的通解．

解 因为矩阵A的第一行元素a，b，c不全为零，所以r（A）≥1．又因为AB＝O，所以

r（A）＋r（B）≤3，

且矩阵B的列向量η1＝［1，2，3］T与η2＝［3，6，k］T都是齐次线性方程组Ax＝0的解．

当k≠9时，η1与η2线性无关，即r（B）＝2，从而r（A）＝1．此时Ax＝0的通解为

x＝c1η1＋c2η2，

式中，c1，c2为任意常数；

当k＝9时，r（B）＝1，矩阵A的秩有两种可能：r（A）＝1或r（A）＝2．以下分别进行讨论．

若r（A）＝2，则方程组Ax＝0的基础解系只含一个解向量，即为η1＝［1，2，3］T，所以通解为

x＝c3η1，

式中，c3为任意常数．

若r（A）＝1，则方程组Ax＝0的基础解系含两个线性无关的解向量．此时方程组Ax＝0与ax1＋bx2＋cx3＝0同解．因为a，b，c不全为零，不妨设a≠0，得两个线性无关的解

ξ1＝［－b，a，0］T，ξ2＝［－c，0，a］T，

于是，方程组Ax＝0的通解为x＝c4ξ1＋c5ξ2，式中，c4，c5为任意常数．

综上，线性方程组Ax＝0的通解为（以下c1，c2，c3，c4，c5均为任意常数）：当k≠9时，x＝c1［1，2，3］T＋c2［3，6，k］T．

当k＝9时，若r（A）＝2，则通解为x＝c3［1，2，3］T；若r（A）＝1，则通解为x＝c4［－b，a，0］T＋c5［－c，0，a］T．

求一个齐次线性方程组，使它的基础解系为α1＝［0，1，2，3］T，α2＝［3，2，1，0］T．

分析 设所求齐次线性方程组为Ax＝0，首先考虑此方程组的方程个数及未知数的个数．因α1是4维列向量，故方程组有4个未知数，即矩阵A的列数为4；另一方面，因基础解系中含2个解，故n－r（A）＝4－r（A）＝2，于是r（A）＝2，则方程的个数（即A的行数）≥2．这样，我们只需构造一个满足题设要求而行数又最少的矩阵，即秩为2的一个2×4矩阵即可．

解 由α1，α2是Ax＝0的解，知A［α1，α2］＝O，则［α1，α2］T AT＝O，于是AT的每一列（即A的行）都是方程组［α1，α2］T x＝0的解，又［α1，α2］T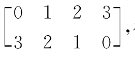＝得基础解系为ξ1＝［1，－2，1，0］T，ξ2＝［2，－3，0，1］T，故A可取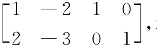对应的齐次线性方程组为

类型三：基础解系

已知η1，η2，η3，η4是Ax＝0的基础解系，则此方程组的基础解系还可以选用（ ）．

（A）η1＋η2，η2＋η3，η3＋η4，η4＋η1

（B）与η1，η2，η3，η4等价的向量组α1，α2，α3，α4

（C）与η1，η2，η3，η4等秩的向量组α1，α2，α3，α4

（D）η1＋η2，η2＋η3，η3－η4，η4－η1

答案（B）

解析 选项（A），（D），由

（η1＋η2）－（η2＋η3）＋（η3＋η4）－（η4＋η1）＝0，

（η1＋η2）－（η2＋η3）＋（η3－η4）＋（η4－η1）＝0，

知（A），（D）均线性相关．选项（C），因为等秩不能保证αi是方程组的解，也就不一定是基础解系．选项（B），由等价知α1，α2，α3，α4是解，由r（α1，α2，α3，α4）＝r（η1，η2，η3，η4）＝4，知α1，α2，α3，α4线性无关，故（B）正确．

设α1，α2，α3是齐次线性方程组Ax＝0的一个基础解系．证明α1＋α2，α2＋α3，α3＋α1也是该方程组的一个基础解系．

证明 由于α1，α2，α3都是Ax＝0的解，故α1＋α2，α2＋α3，α3＋α1也都是Ax＝0的解．若存在数k1，k2，k3，使k1（α1＋α2）＋k2（α2＋α3）＋k3（α3＋α1）＝0，则有

由于α1，α2，α3线性无关，故得故方程组（*）有唯一解k1＝k2＝k3＝0，从而α1＋α2，α2＋α3，α3＋α1线性无关．

由题设知Ax＝0的基础解系含3个解向量，故α1＋α2，α2＋α3，α3＋α1也是Ax＝0的一个基础解系．

考点17 非齐次线性方程组

1．解的判定

对m个方程、n个未知数的非齐次线性方程组

即Am×n x＝b．

（1）Am×n x＝b无解⇔r（A）≠r A┊（b）⇔r（A）＋1＝r A┊（b）；

（2）Am×n x＝b有唯一解⇔r（A）＝r A┊（b）＝n（未知数个数、A的列数）；

（3）Am×n x＝b有无穷多解⇔r（A）＝r A┊（b）＜n（未知数个数、A的列数）．

2．解的性质

（1）若η1，η2都是Ax＝b的解，ξ是Ax＝0的解，则η1－η2是Ax＝0的解，η1＋kξ是Ax＝b的解．

（2）若η1，η2，…，ηs都是Ax＝b的解，则当

当Am×n x＝b有无穷多解时，其通解为η＋k1ξ1＋k2ξ2＋…＋ktξt，其中k1，k2，…，kt是任意常数．这里η是Ax＝b的一个解，ξ1，ξ2，…，ξt是Ax＝0的基础解系．

类型一：解的判定

已知方程组

答案－1

解析 非齐次线性方程组无解的充要条件是系数矩阵的秩不等于增广矩阵的秩．对于未知数个数与方程个数相等的方程组来说，可先考查系数矩阵的行列式为零的情形，解得a＝－1或3．当满足上述条件时，方程组无解或有无穷多解，所以应进一步考查是哪种情形．当a＝－1时，系数矩阵的秩为2，增广矩阵的秩为3，故方程组无解；当a＝3时，系数矩阵的秩为2，增广矩阵的秩也为2，故方程组有无穷多解，因而，a＝3不符合条件．

设

证明 三直线

相交于一点的充要条件是向量组a，b线性无关，且向量组a，b，c线性相关．

（1）a，b为何值时，方程组有解？

（2）方程组有解时，求出方程组的导出组的一个基础解系；

（3）方程组有解时，求出方程组的全部解．

解 对方程组（*）的增广矩阵作初等行变换，有

（1）当b－3a＝0且2－2a＝0，即a＝1，b＝3时，r（A）＝r（B）＝2，此时方程组有解．

（2）当a＝1且b＝3时，原方程组的同解方程组为

（3）在方程组（**）中，令x3＝x4＝x5＝0，得（*）的一个特解u＝［－2，3，0，0，0］T．于是原方程组的全部解为

式中，k1，k2，k3为任意常数．

λ取何值时，方程组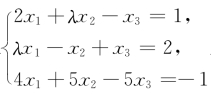无解，有唯一解或有无穷多解，并在有无穷多解时写出方程组的通解．

解 原方程组的系数行列式为

故当λ≠1且时，方程组有唯一解．

当λ＝1时，原方程组为

对其增广矩阵作初等行变换，有

因此，当λ＝1时，原方程组有无穷多解，其通解为

或［x1，x2，x3］T＝［1，－1，0］T＋k［0，1，1］T，式中，k为任意常数．(www.xing528.com)

当时，原方程组的同解方程组为

对其增广矩阵作初等行变换，有

由此可知当时，原方程组无解．

已知非齐次线性方程组

有三个线性无关的解．

（1）证明方程组系数矩阵A的秩r（A）＝2；

（2）求a，b的值及方程组的通解．

（1）证明设ξ1，ξ2，ξ3是题设所给非齐次线性方程组的三个线性无关的解向量，则ξ2－ξ1，ξ3－ξ1是其对应的齐次线性方程组Ax＝0的两个线性无关的解．若令t表示方程组Ax＝0的基础解系所含向量的个数，则t≥2．又由r（A）＋t＝4得4－r（A）≥2，即r（A）≤2．不难看到，在矩阵A中有一个2阶子式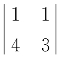＝－1≠0（或矩阵A有两行（列）线性无关），所以r（A）≥2，从而r（A）＝2．

（2）解对非齐次线性方程组的增广矩阵

作初等行变换：

由题设和（1）知＝2，故有

4－2a＝0，4a＋b－5＝0，

从而得a＝2，b＝－3．

此时有

可得方程组的通解为

式中，k1，k2为任意常数．

设线性方程组

已知［1，－1，1，－1］T是该方程组的一个解．

（1）求方程组的全部解，并用对应的齐次线性方程组的基础解系表示；

（2）求该方程组满足x2＝x3的全部解．

分析 含未知参数的线性方程组的求解，当系数矩阵不是方阵时，一般用初等行变换化增广矩阵为阶梯形，然后对参数进行讨论．由于已知方程组的一个解，于是可先由它来（部分）确定未知参数．

解 将［1，－1，1，－1］T代入方程组，得λ＝μ．对方程组的增广矩阵施以初等行变换，得

此时r（A）＝r（A）＝3＜4，故方程组有无穷多解，且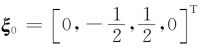为其一个特解，对应的齐次线性方程组的基础解系为ξ＝［－2，1，－1，2］T，故方程组的全部解为

式中，k为任意常数．

当时，有

此时r（A）＝＝2＜4，故方程组有无穷多解，且为其一个特解，对应的齐次线性方程组的基础解系为ξ1＝［1，－3，1，0］T，ξ2＝［－1，－2，0，2］T．

故方程组的全部解为x＝η0＋k1ξ1＋k2ξ2，即

式中，k1，k2为任意常数．

①本例所求的全部解表达式均不唯一．

a．题设中已给出方程组的特解，而在（1），（2）两小题的计算中取了其他特解，如果（1），（2）两小题的特解均改用［1，－1，1，－1］T，当然也是正确的．

b．第（2）小题当时推得关系式

1－3k1－2k2＝k1，

据此，也可解得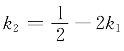，此时原方程组满足x2＝x3的解也可表示为

式中，k1为任意常数．

②本例的第（2）小题其实就是求原方程组与方程x2＝x3的公共解．求两个线性方程组的公共解也是一类基本题型，此类题型将在考点18中讨论．

类型三：抽象型

设A是秩为3的5×4矩阵，α1，α2，α3是非齐次线性方程组Ax＝b的3个不同的解，若α1＋α2＋2α3＝［2，0，0，0］T，3α1＋α2＝［2，4，6，8］T，则Ax＝b的通解是__________．

答案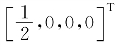＋k［0，2，3，4］T（k是任意常数）

解析 由于r（A）＝3，所以齐次线性方程组Ax＝0的基础解系有4－r（A）＝1个线性无关的解向量．又因为

（α1＋α2＋2α3）－（3α1＋α2）＝2（α3－α1）＝［0，－4，－6，－8］T

是Ax＝0的解，故其基础解系可以用［0，2，3，4］T表示．由

A（α1＋α2＋2α3）＝Aα1＋Aα2＋2Aα3＝4b，

知是方程组Ax＝b的一个解．故由非齐次线性方程组解的结构知其通解是

本题考查方程组解的性质与解的结构，要会用“减”的方法求齐次线性方程组的解，用“除”的方法求非齐次线性方程组的解．

已知4阶方阵A＝［α1，α2，α3，α4］，α1，α2，α3，α4均为4维列向量，其中α2，α3，α4线性无关，α1＝2α2－α3．如果β＝α1＋α2＋α3＋α4，求线性方程组Ax＝β的通解．

解 由于α2，α3，α4线性无关，α1＝2α2－α3，则r（A）＝r（α1，α2，α3，α4）＝3，故Ax＝0的基础解系只有1个线性无关的解向量，而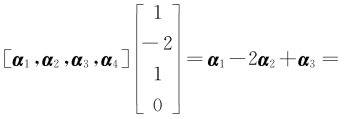0，所以［1，－2，1，0］T是Ax＝0的一个基础解系，而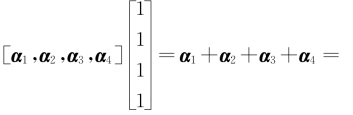β，所以［1，1，1，1］T是Ax＝β的一个特解，于是Ax＝β的通解为［1，1，1，1］T＋k［1，－2，1，0］T，其中k是任意常数．

类型四：先化简，再求解

设α＝

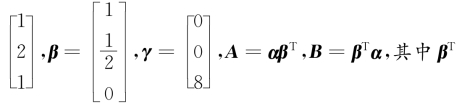是β的转置，求解方程组

2B2A2x＝A4x＋B4x＋γ．

解 由题设得

代入原方程，得

16Ax＝8Ax＋16x＋γ，

即8（A－2E）x＝γ（其中E是3阶单位矩阵）．

令x＝［x1，x2，x3］T，代入上式，得到非齐次线性方程组

解 其对应的齐次线性方程组，得通解

显然，非齐次线性方程组的一个特解为

于是所求方程组的解为

式中，k为任意常数．

类型五：矩阵方程

设A，B，X均是3阶矩阵，其中

（1）a取何值时，矩阵方程AX－B＝BX无解；

（2）a取何值时，矩阵方程AX－B＝BX有解，有解时，求全部解．

解 由题设条件知，矩阵方程为（A－B）X＝B，其中

将X和B以列分块，记X＝［x1，x2，x3］，B＝［β1，β2，β3］，则矩阵方程为

（A－B）xi＝βi，i＝1，2，3．

对增广矩阵［A－B┊B］作初等行变换，有

（1）当a＝－1时，r（A－B）＝2≠r（A－B┊B）＝3，矩阵方程无解．

（2）当a≠－1时，r（A－B）＝3＝r（A－B┊B）＝3，矩阵方程有解且仅有唯一解．

考点18 公共解与同解

若Ax＝0的解都是Bx＝0的解，且Bx＝0的解也都是Ax＝0的解，则称Ax＝0和Bx＝0同解；

若α（非零）是Ax＝0的解，也是Bx＝0的解，则称α是Ax＝0和Bx＝0的非零公共解．

（1）Ax＝0和Bx＝0同解⇒r（A）＝r（B）．

（因Ax＝0和Bx＝0同解，则Ax＝0和Bx＝0的基础解系中所含线性无关解的个数相同，于是n－r（A）＝n－r（B），即r（A）＝r（B），注意不可由r（A）＝r（B）反推Ax＝0和Bx＝0同解）

（2）Ax＝0和Bx＝0同解⇔Ax＝0的解都是Bx＝0的解，且r（A）＝r（B）．

（3）Ax＝0和Bx＝0同解⇔r（A）＝r（B）＝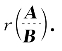

（4）Ax＝0和Bx＝0同解⇔A的行向量组与B的行向量组等价．

（5）设A是m×n矩阵，则Ax＝0和（AT A ）x＝0是同解方程组．

（6）设A是n阶矩阵，则An x＝0和An＋1x＝0是同解方程组．

已知方程组

（1）求解方程组（Ⅰ）；

（2）求m，n，t为何值时，方程组（Ⅰ）与方程组（Ⅱ）同解．

分析 （1）对（Ⅰ）的增广矩阵作初等行变换，计算它的通解．

（2）将（Ⅰ）的通解代入（Ⅱ）的各个方程，即可得出参数m，n，t的值．

解 （1）对（Ⅰ）的增广矩阵作初等行变换，有

所以（Ⅰ）的通解为

［x1，x2，x3，x4］T＝C［1，1，2，1］T＋［－2，－4，－5，0］T，

式中，C为任意常数．

（2）由（1）知x1＝C－2，x2＝C－4，x3＝2C－5，x4＝C，将其代入（Ⅱ）的各个方程，整理得

令C＝0，解得m＝2，n＝4，t＝6．

当m＝2，n＝4，t＝6时，代入方程组（Ⅱ），有

对其增广矩阵作初等行变换，有

由此可知，当m＝2，n＝4，t＝6时方程组（Ⅰ）与（Ⅱ）同解．

本题（2）的解答中，应注意的是：当（Ⅰ）的通解代入（Ⅱ）后得到m＝2，n＝4，t＝6．至此问题并没有解完，接着还要证明当m＝2，n＝4，t＝6时，（Ⅱ）的所有解都是（Ⅰ）的解，题解中是通过对（Ⅱ）的增广矩阵作若干次初等行变换得到的行最简形矩阵与（Ⅰ）的相同给出这一证明的．

已知齐次线性方程组

同解，求a，b，c的值．

解 由于方程组（Ⅱ）的未知量个数大于方程的个数，故方程组（Ⅱ）有无穷多解．又方程组（Ⅰ）与（Ⅱ）同解，所以方程组（Ⅰ）的系数矩阵的秩小于3．

对方程组（Ⅰ）的系数矩阵作初等行变换，有

从而a＝2．

此时，方程组（Ⅰ）的系数矩阵可化为

故［－1，－1，1］T是方程组（Ⅰ）的一个基础解系．

将x1＝－1，x2＝－1，x3＝1代入方程组（Ⅱ），可得b＝1，c＝2或b＝0，c＝1．

当b＝1，c＝2时，对方程组（Ⅱ）的系数矩阵作初等行变换，有

故方程组（Ⅰ）与（Ⅱ）同解；

当b＝0，c＝1时，对方程组（Ⅱ）的系数矩阵作初等行变换，有

知方程组（Ⅰ）与（Ⅱ）的解不完全相同．

综上所述，当a＝2，b＝1，c＝2时，方程组（Ⅰ）与（Ⅱ）同解．

设四元齐次线性方程组

（1）求方程组（Ⅰ）与（Ⅱ）的基础解系；

（2）求方程组（Ⅰ）与（Ⅱ）的公共解．

解 （1）对方程组（Ⅰ）的系数矩阵作初等行变换，有

故ξ1，ξ2为方程组（Ⅰ）的基础解系．

对方程组（Ⅱ）的系数矩阵作初等行变换，有

故η1，η2为方程组（Ⅱ）的基础解系．

（2）解法1 Ax＝0和Bx＝0的公共解是既满足Ax＝0又满足Bx＝0的解，即是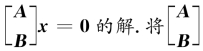作初等行变换化为行最简形矩阵．

解 法2 Ax＝0和Bx＝0的公共解是Ax＝0通解中满足Bx＝0的那部分解．

由（1）知Ax＝0的基础解系为ξ1＝［0，0，1，0］T，ξ2＝［－1，1，0，1］T，通解为

将通解代入方程组（Ⅱ），得

代入方程组（Ⅰ）的通解得方程组（Ⅰ），（Ⅱ）的公共解为

（显然Ax＝0和Bx＝0的公共解也是Bx＝0的通解中满足Ax＝0的那部分解，留给读者作为练习）

解 法3 Ax＝0，Bx＝0的公共解是Ax＝0的通解与Bx＝0的通解中相同部分（即相等）的解．

由（1）知方程组Ax＝0的通解为

方程组Bx＝0的通解为

将k1＝－2c，k2＝－c代入k1ξ1＋k2ξ2，得公共解为

本题（2）中求两个方程组的公共解提供了三种解法，当然求两个方程组的公共解有很多种命题方法．

①已知Ax＝0及Bx＝0，求公共解；

②已知Ax＝0及Bx＝0的通解k1ξ1＋k2ξ2，求公共解；

③已知Ax＝0的通解k1η1＋k2η2，Bx＝0的通解λ1ξ1＋λ2ξ2，求公共解．

已知齐次线性方程组（Ⅰ）的基础解系为ξ1＝［1，0，1，1］T，ξ2＝［2，1，0，－1］T，ξ3＝［0，2，1，－1］T，添加两个方程

后组成齐次线性方程组（Ⅱ）．求（Ⅱ）的基础解系．

分析 先将（Ⅰ）的通解代入添加的两个方程中，得到（Ⅱ）的通解，然后由此通解求得（Ⅱ）的基础解系．

解 由题设知（Ⅰ）的通解为

［x1，x2，x3，x4］T＝C1ξ1＋C2ξ2＋C3ξ3＝［C1＋2C2，C2＋2C3，C1＋C3，C1－C2－C3］T，

即x1＝C1＋2C2，x2＝C2＋2C3，x3＝C1＋C3，x4＝C1－C2－C3，

将它们代入添加的两个方程中，得

即3C1＋2C2＋2C3＝0，整理得

将上式代入（Ⅰ）的通解，得

从题解中可以看到，（Ⅰ）的通解中含有3个任意常数，而（Ⅱ）的通解中只包含两个任意常数，这是C1，C2，C3受添加的两个方程，即3C1＋2C2＋2C3＝0约束的结果．