向量的线性相关与线性无关概念题

向量的概念 向量的线性组合和线性表示 向量组的线性相关与线性无关 向量组的极大线性无关组 等价向量组 向量组的秩 向量组的秩与矩阵的秩之间的关系 向量的内积 线性无关向量组的正交规范化方法

1．理解n维向量、向量的线性组合与线性表示的概念．

2．理解向量组线性相关、线性无关的概念，掌握向量组线性相关、线性无关的有关性质及判别法．

3．了解向量组的极大线性无关组和向量组的秩的概念，会求向量组的极大线性无关组及秩．

4．了解向量组等价的概念，了解矩阵的秩与其行（列）向量组的秩的关系．

5．了解内积的概念，掌握线性无关向量组正交规范化的施密特（Schmidt）方法．

1.向量组的线性相关与线性无关（考点13）

这部分比较抽象，证明题较多，考生要在理解线性相关与线性无关概念的基础上，把握具体型（含参数）向量组线性相关与线性无关的判定，掌握用定义法与秩的方法处理线性相关与线性无关的证明题．

2.线性表示（考点14）

这部分主要以含参数的计算题居多，本质上就是判断非齐次线性方程组有解（能线性表示）还是无解（不能线性表示）的问题．

3.极大线性无关组及向量组的秩（考点15）

极大线性无关组的引入使得我们对向量组的认识更深入了一步，实际上，研究一个向量组只需研究它的极大线性无关组，要会找极大线性无关组，并会用极大线性无关组表示其余向量；向量组的秩虽与矩阵的秩在定义上有所不同（前者是借助极大线性无关组，后者是借助行列式），但在数值上二者又是一致的（矩阵的秩＝矩阵列向量组的秩＝矩阵行向量组的秩）．

考点13 向量的概念及相关性

1．向量的概念

n个数a1，a2，…，an组成的有序数组α＝［a1，a2，…，an］T或α＝［a1，a2，…，an］叫作n维向量，其中a1，a2，…，an叫作向量α的坐标分量，前一个叫n维列向量，后一个叫n维行向量．对两个n维向量α＝［a1，a2，…，an］T，β＝［b1，b2，…，bn］T，α＝β⇔ai＝bi（i＝1，2，…，n）．

则称这些列向量α1，α2，…，αn为矩阵A的列向量组．同理，可给出A的行向量组的概念．

2．向量的运算

设α＝［a1，a2，…，an］T，β＝［b1，b2，…，bn］T，则

加法 α＋β＝［a1＋b1，a2＋b2，…，an＋bn］T；

数乘 kα＝［ka1，ka2，…，kan］T；

内积 （α，β）＝αTβ＝βTα＝a1b1＋a2b2＋…＋anbn，特别地，αTα＝0⇔α＝0；

正交 若αTβ＝0，称α与β正交；

模 则称α为单位列向量．

3．线性相关与线性无关

对向量组α1，α2，…，αs，若存在一组不全为零的数k1，k2，…，ks，使k1α1＋k2α2＋…＋ksαs＝0，则称向量组α1，α2，…，αs线性相关，否则称线性无关．

线性无关 如果k1α1＋k2α2＋…＋ksαs＝0，则必有k1＝k2＝…＝ks＝0；或只要有一个ki≠0，必会有k1α1＋k2α2＋…＋ksαs≠0．

含有零向量的向量组必相关；含有相等或成比例向量的向量组必相关；一个向量不为0，则无关；两个向量不成比例，则无关；三个向量不共面，则无关．

类型一：线性相关与线性无关的概念题

设α1，α2，…，αm均为n维向量，下列结论正确的是（ ）．

（A）若k1α1＋k2α2＋…＋kmαm＝0，则α1，α2，…，αm线性相关

（B）若对任意一组不全为零的数k1，k2，…，km，都有k1α1＋k2α2＋…＋kmαm≠0，则α1，α2，…，αm线性无关

（C）若α1，α2，…，αm线性相关，则对任意一组不全为零的数k1，k2，…，km，都有k1α1＋k2α2＋…＋kmαm＝0

（D）若0α1＋0α2＋…＋0αm＝0，则α1，α2，…，αm线性无关

答案（B）

解析 考虑选项（B）．（下面考虑其逆否命题）假设α1，α2，…，αm线性相关，则必存在一组不全为零的数k1，k2，…，km，使得k1α1＋k2α2＋…＋kmαm＝0．它显然为真．

又选项（B）为其逆否命题，它们同真同假，知（B）为真，故选（B）．

顺便指出，其余3个选项不正确的原因分别是：

选项（A）中没有指明k1，k2，…，km不全为0；

选项（C）中需将“对任意”改为“存在”，同时把“都”字去掉才正确；

选项（D）中的结论对于线性相关的向量组亦成立．

已知α1，α2，β1，β2均是n（n≥2）维向量，则（ ）．

（A）α1，α2线性无关，β1，β2线性无关，必有α1＋β1，α2＋β2线性无关

（B）α1，α2线性相关，β1，β2线性相关，必有α1＋β1，α2＋β2线性相关

（C）α1，α2线性无关，β1，β2线性相关，必有α1＋β1，α2＋β2线性无关

（D）α1，α2线性相关，β1，β2线性无关，则α1＋β1，α2＋β2可能线性相关，可能线性无关

答案（D）

由排除法，知（D）成立，亦可直接举出两个方面的例子（请读者举例），故选（D）．

类型二：线性相关与线性无关的计算（判断）题

向量组α1，α2，…，αs线性相关⇔齐次线性方程组［α1，α2，…，αs］x＝0有非零解⇔r（α1，α2，…，αs）＜s（向量个数、未知数个数）．

向量组α1，α2，…，αs线性无关⇔齐次线性方程组［α1，α2，…，αs］x＝0只有零解⇔r（α1，α2，…，αs）＝s（向量个数、未知数个数）．

推论1 n个n维向量α1，α2，…，αn线性相关（无关）⇔

推论2 n＋1个n维向量必线性相关．

（1）设α1＝［1，－1，2，1］T，α2＝［2，－1，3，a］T，α3＝［0，1，－1，1］T线性相关，则a＝__________；

（2）设α1＝［a，1，1］T，α2＝［1，a，1］T，α3＝［1，1，a］T线性无关，则a≠__________．

答案（1）3；（2）－2和1

解析 （1）α1，α2，α3线性相关⇔r（α1，α2，α3）＜3，而

故当a＝3时，r（α1，α2，α3）＝2＜3，此时α1，α2，α3线性相关．

如，设α1＝［1，2，3］T，α2＝［0，4，5］T，α3＝［0，0，6］T，由α3线性无关；那么，去掉α3剩余的α1，α2仍线性无关，对应增加坐标后的β1＝［1，2，x1，3］T，β2＝［0，4，y1，5］T，β3＝［0，0，z1，6］T仍线性无关．

已知n维列向量组α1，α2，…，αs线性无关，则向量组α′1，α′2，…，α′s可能线性相关的是（ ）．

（A）α′i（i＝1，2，…，s）是αi（i＝1，2，…，s）中第一个分量加到第二个分量得到的向量

（B）α′i（i＝1，2，…，s）是αi（i＝1，2，…，s）中第一个分量改变成其相反数的向量

（C）α′i（i＝1，2，…，s）是αi（i＝1，2，…，s）中第一个分量改为0的向量

（D）α′i（i＝1，2，…，s）是αi（i＝1，2，…，s）中在第n个分量后增添一个分量的向量

答案（C）

解析 将向量的第一个分量均变为0，相当于减少一个分量，此时新向量组可能变为线性相关，选（C）．选项（A），（B）属初等（行）变换，不改变矩阵的秩，并未改变列向量组的线性相关性，选项（D）增加向量分量也不改变线性相关性．

类型三：线性相关与线性无关的证明题

如何证明向量组α1，α2，…，αs线性无关．

定义法：设k1α1＋k2α2＋…＋ksαs＝0⇒必有k1＝k2＝…＝ks＝0；

秩

设向量组α1，α2，α3线性无关，且

当km－1≠0，即km≠1时，向量组kα2－α1，mα3－α2，α1－α3线性无关；

当km－1＝0，即km＝1时，向量组kα2－α1，mα3－α2，α1－α3线性相关．

设α1，α2，α3为两两正交的非零向量，证明：α1，α2，α3线性无关．

证明 设有一组常数k1，k2，k3，使

k1α1＋k2α2＋k3α3＝0，

两边与α1作内积，由（α1，α2）＝0，（α1，α3）＝0得

k1（α1，α1）＋k2（α1，α2）＋k3（α1，α3）＝k1（α1，α1）＝0，

又因为α1≠0，（α1，α1）＞0，故k1＝0．

同理可得k2＝0，k3＝0，故α1，α2，α3线性无关．

设A是n阶矩阵，若存在正整数k，使Akα＝0，且Ak－1α≠0．证明：α，Aα，…，Ak－1α线性无关．

证明 设有一组常数λ1，λ2，…，λk，使得

式①两边左乘Ak－1，得

由题设条件Akα＝0，故Ak＋1α＝Ak＋2α＝…＝A2k－2α＝0，从而得

由于Ak－1α≠0，故λ1＝0，代入式①得

将式③两边左乘Ak－2，同上可证λ2＝0．

同理可证λ3＝λ4＝…＝λk＝0，从而得证α，Aα，…，Ak－1α线性无关．

设A是n阶矩阵，α1，α2，α3是n维非零列向量，且Aα1＝kα1，Aα2＝lα1＋kα2，Aα3＝lα2＋kα3，其中l≠0，证明：α1，α2，α3线性无关．

分析 对k1α1＋k2α2＋k3α3＝0，如何证明组合系数k1＝k2＝k3＝0呢？要作恒等变形就应仔细分析已知条件，Aαi的条件其实就是

（A－k E）α1＝0，（A－k E）α2＝lα1，（A－k E）α3＝lα2．

这启发我们应用A－k E左乘来作恒等变形．

证明 设有一组数k1，k2，k3，使得

k1α1＋k2α2＋k3α3＝0，

两边同时左乘A－k E，有

k1（A－k E）α1＋k2（A－k E）α2＋k3（A－k E）α3＝0，

即k2lα1＋k3lα2＝0，亦即

k2α1＋k3α2＝0，

两边同时左乘A－k E，可得k3α1＝0．

由α1≠0，故必有k3＝0，依次往上代入得k2＝0，k1＝0，所以α1，α2，α3线性无关．

设A是m×n矩阵，B是n×m矩阵，且BA＝E．证明：A的列向量组线性无关．

证明 （用秩）只需证明r（A）＝n即可．由n＝r（En）＝r（BA）≤r（A）≤n，知r（A）＝n，于是A的列向量组线性无关．（这里秩的每一步理由要想清楚）

设A，B为满足AB＝O的任意两个非零矩阵，则必有（ ）．

（A）A的列向量组线性相关，B的行向量组线性相关

（B）A的列向量组线性相关，B的列向量组线性相关

（C）A的行向量组线性相关，B的行向量组线性相关

（D）A的行向量组线性相关，B的列向量组线性相关

答案（A）

解析 不妨设Am×n，Bn×s，由AB＝O，得r（A）＋r（B）≤n，又A≠O，B≠O，则r（A）≥1，r（B）≥1，于是r（Am×）n＝r（α1，α2，…，αn）（这里α1，α2，…，αn即A的列向量组）＜n（向量个数），故向量组α1，α2，…，αn线性相关，即A的列向量组线性相关；(www.xing528.com)

同理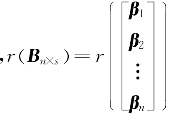（这里β1，β2，…，βn即B的行向量组）＜n（向量个数），故向量组β1，β2，…，βn线性相关，即B的行向量组线性相关．选（A）．

考点14 线性表示

若存在一组数k1，k2，…，ks，使β＝k1α1＋k2α2＋…＋ksαs，则称向量β能由向量组α1，α2，…，αs线性表示．

设有两个向量组（Ⅰ）α1，α2，…，αs和（Ⅱ）β1，β2，…，βt，若向量组（Ⅱ）中每个向量βi（i＝1，2，…，t）都能由向量组（Ⅰ）线性表示，则称向量组（Ⅱ）能由向量组（Ⅰ）线性表示；若向量组（Ⅰ）和向量组（Ⅱ）可相互线性表示，则称这两个向量组等价．

β能由向量组α1，α2，…，αs线性表示

⇔非齐次线性方程组［α1，α2，…，αs］x＝β有解

⇔r（α1，α2，…，αs）＝r（α1，α2，…，αs，β）．

β不能由向量组α1，α2，…，αs线性表示

⇔非齐次线性方程组［α1，α2，…，αs］x＝β无解

⇔r（α1，α2，…，αs）≠r（α1，α2，…，αs，β）．

若向量组α1，α2，…，αs线性无关，而α1，α2，…，αs，β线性相关，则β可由α1，α2，…，αs线性表示，且表示式唯一．

若向量组α1，α2，…，αs可由向量组β1，β2，…，βt线性表示，且s＞t，则α1，α2，…，αs线性相关．此定理可简单叙述为“以少表多，多必相关”，如β1＝2α1－α2，β2＝α1＋α2，β3＝－α1＋3α2，这里是用两个α1，α2表示了三个β1，β2，β3，则向量组β1，β2，β3一定是线性相关的．

已知α1＝［1，4，0，2］T，α2＝［2，7，1，3］T，α3＝［0，1，－1，a］T，β＝［3，10，b，4］T，问

（1）a，b取何值时，β不能由α1，α2，α3线性表示？

（2）a，b取何值时，β可由α1，α2，α3线性表示？并写出此表达式．

解 对矩阵［α1，α2，α3，β］作初等行变换，有

（1）当b≠2时，线性方程组［α1，α2，α3］x＝β无解，此时β不能由α1，α2，α3线性表示．

（2）当b＝2，a≠1时，线性方程组［α1，α2，α3］x＝β有唯一解，其解为

x＝［x1，x2，x3］T＝［－1，2，0］T，

于是β可唯一表示为β＝－α1＋2α2；

当b＝2，a＝1时，线性方程组［α1，α2，α3］x＝β有无穷多解，其通解为

x＝［x1，x2，x3］T＝k［－2，1，1］T＋［－1，2，0］T，

式中，k为任意常数，这时β可由α1，α2，α3线性表示为

β＝－（2k＋1）α1＋（k＋2）α2＋kα3．

设α1＝［1，2，1］T，α2＝［2，3，a］T，α3＝［1，a＋2，－2］T，若β1＝［1，3，4］T能由α1，α2，α3线性表示，而β2＝［0，1，2］T不能由α1，α2，α3线性表示，则a＝__________．

答案－1

解析 依题意，方程组x1α1＋x2α2＋x3α3＝β1有解，而方程组x1α1＋x2α2＋x3α3＝β2无解．因为两个方程组的系数矩阵相同，故可合并一起加减消元，即

可见当a＝－1时，方程组x1α1＋x2α2＋x3α3＝β1有解，而x1α1＋x2α2＋x3α3＝β2无解，故a＝－1．

设向量组α1，α2，α3线性相关，向量组α2，α3，α4线性无关，问：

（1）α1能否由α2，α3线性表示？证明你的结论；

（2）α4能否由α1，α2，α3线性表示？证明你的结论．

解 （1）α1能由α2，α3线性表示．理由如下：

由已知α2，α3，α4线性无关，故α2，α3线性无关．又α1，α2，α3线性相关，故α1可由α2，α3线性表示．

（2）α4不能由α1，α2，α3线性表示．理由如下：

（反证）设α4可由α1，α2，α3线性表示，即

α4＝λ1α1＋λ2α2＋λ3α3，

由（1）知α1＝μ2α2＋μ3α3，代入上式，得

α4＝λ1（μ2α2＋μ3α3）＋λ2α2＋λ3α3＝（λ1μ2＋λ2）α2＋（λ1μ3＋λ3）α3，

α4可由α2，α3线性表示，从而α2，α3，α4线性相关，与已知矛盾．因此，α4不能由α1，α2，α3线性表示．

（1）设α1，α2，β1，β2都是3维列向量，且α1，α2线性无关，β1，β2线性无关，证明存在3维非零列向量ξ，使得ξ既可由α1，α2线性表示，又可由β1，β2线性表示；

（2）当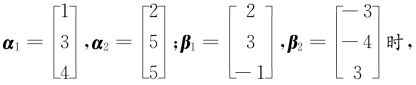求所有既可由α1，α2线性表示，又可由β1，β2线性表示的向量ξ．

分析 （1）由α1，α2，β1，β2线性相关知，存在不全为零的数k1，k2，k3，k4，使得

k1α1＋k2α2＋k3β1＋k4β2＝0，

于是，取ξ＝k1α1＋k2α2即可．

（2）由（1）知，对所给的α1，α2，只要确定k1，k2即可，而k1，k2应满足k1α1＋k2α2＋k3β1＋k4β2＝0，将具体的α1，α2，β1，β2代入方程组，解之可得k1，k2，从而得到ξ．

（1）证明由于α1，α2，β1，β2都是3维列向量，所以α1，α2，β1，β2线性相关，于是存在不全为零的数k1，k2，k3，k4，使得

记ξ＝k1α1＋k2α2，则ξ是非零向量（若ξ＝0，则有k1α1＋k2α2＝0，由于α1，α2线性无关，所以k1＝k2＝0，即由式①得k3β1＋k4β2＝0．由于β1，β2线性无关，所以k3＝k4＝0．这样与k1，k2，k3，k4不全为零矛盾），并且ξ＝－k3β1－k4β2．由此证明了存在非零列向量ξ，它既可由α1，α2线性表示，又可由β1，β2线性表示．

（2）解由（1）知

且k1，k2满足

k1α1＋k2α2＋k3β1＋k4β2＝0，

将具体的α1，α2，β1，β2代入得方程组，有

对系数矩阵施行初等行变换得

于是，该方程组的基础解系为［4，－3，1，0］T和［－7，5，0，1］T，故通解为

λ1［4，－3，1，0］T＋λ2［－7，5，0，1］T＝［4λ1－7λ2，－3λ1＋5λ2，λ1，λ2］T．

由此得k1＝4λ1－7λ2，k2＝－3λ1＋5λ2，代入ξ＝k1α1＋k2α2得

式中，λ1，λ2是任意常数．

本题求解的关键是4个3维列向量α1，α2，β1，β2必然相关．

确定常数a，使向量组α1＝［1，1，a］T，α2＝［1，a，1］T，α3＝［a，1，1］T可由向量组β1＝［1，1，a］T，β2＝［－2，a，4］T，β3＝［－2，a，a］T线性表示，但向量组β1，β2，β3不能由向量组α1，α2，α3线性表示．

解 记A＝［α1，α2，α3］，B＝［β1，β2，β3］．由于β1，β2，β3不能由α1，α2，α3线性表示，所以r（A）＜3，从而

得a＝1或a＝－2．

当a＝1时，α1＝α2＝α3＝β1＝［1，1，1］T，显然α1，α2，α3可由β1，β2，β3线性表示，而β2＝［－2，1，4］T不能由α1，α2，α3线性表示，即a＝1符合题意；

当a＝－2时，则有

考虑非齐次线性方程组Bx＝α2，由上述增广矩阵可知r（B）＝2，而r（［B┊α2］）＝3，则方程组Bx＝α2无解，即α2不能由向量组β1，β2，β3线性表示，所以a＝－2不符合题意，应舍去．综上a＝1．

对A＝［α1，α2，α3］，若r（A）＝3，则α1，α2，α3线性无关，而α1，α2，α3，βi（i＝1，2，3）是4个3维向量，必相关，此时βi（i＝1，2，3）可由α1，α2，α3线性表示，这与题目矛盾，于是r（A）＜3．

考点15 向量组的秩及等价

1．极大线性无关组及向量组的秩

对向量组（Ⅰ）α1，α2，…，αs．若在（Ⅰ）中能选出r个向量αi1，αi2，…，αir满足：

（1）αi1，αi2，…，αir线性无关；

（2）向量组（Ⅰ）中任一向量都能由αi1，αi2，…，αir线性表示．

则称αi1，αi2，…，αir是向量组（Ⅰ）的一个极大线性无关组，简称极大无关组，极大无关组中所含的向量个数r称为向量组（Ⅰ）的秩，记作只有零向量的向量组没有极大无关组，规定秩为0．

①一个线性无关向量组的极大无关组就是其本身；

②任一向量组与它的极大无关组等价；

③一个向量组的极大无关组一般不唯一，但每个极大无关组所含的向量个数是相同的（就是该向量组的秩），且它们之间也都是等价关系．

矩阵的秩等于它的每一列构成的列向量组的秩，也等于它的每一行构成的行向量组的秩．

设向量组β1，β2，…，βt能由向量组α1，α2，…，αs线性表示，则r（β1，β2，…，βt）≤r（α1，α2，…，αs）．

已知向量组α1＝［1，1，1，3］T，α2＝［－a，－1，2，3］T，α3＝［1，2a－1，3，7］T，α4＝［－1，－1，a－1，－1］T的秩为3，则a＝__________．

答案

解析 对A＝［α1，α2，α3，α4］作初等行变换，有

当a＝1时，

此时r（A）＝2，不合题意，故a≠1．于是

则当r（α1，α2，α3，α4）＝3时，即－3a2＋a＋2＝0，又a≠1，故

设向量组α1＝［1，1，1，3］T，α2＝［－1，－3，5，1］T，α3＝［3，2，－1，p＋2］T，α4＝［－2，－6，10，p］T ．

（1）p为何值时，该向量组线性无关？并在此时将向量α＝［4，1，6，10］T用α1，α2，α3，α4线性表示；

（2）p为何值时，该向量组线性相关？并在此时求出它的秩和一个极大线性无关组．

解 对矩阵［α1，α2，α3，α4，α］作初等行变换，有

（1）当p≠2时，向量组α1，α2，α3，α4线性无关，此时设α＝x1α1＋x2α2＋x3α3＋x4α4，解得

（2）当p＝2时，向量组α1，α2，α3，α4线性相关，此时向量组的秩等于3．α1，α2，α3（或α1，α3，α4）为其一个极大线性无关组．

解 对矩阵［α1，α2，α3］施行初等行变换：

由此可知α1，α2，α3的秩为2．

对矩阵［β1，β2，β3］施行初等行变换：

由于r（α1，α2，α3）＝2，所以r（β1，β2，β3）＝2，从而有

容易知道α1，α2是α1，α2，α3的一个极大线性无关组，所以β3也可由α1，α2线性表示，即β3，α1，α2线性相关，从而

即b＝5，将它代入a＝3b，得a＝15．

2．向量组等价

向量组（Ⅰ）α1，α2，…，αs与向量组（Ⅱ）β1，β2，…，βt等价

⇔r（α1，α2，…，αs）＝r（α1，α2，…，αs，β1，β2，…，βt）＝r（β1，β2，…，βt）

⇔向量组（Ⅰ）α1，α2，…，αs可由向量组（Ⅱ）β1，β2，…，βt线性表示，且

由r（A）＝r（B）＝r（A，B）知，应取a＝1，b＝2，c＝－2，此时α1，α2，α3与β1，β2，β3等价．

设A，B，C均为n阶矩阵，若AB＝C，且B可逆，则（ ）．

（A）矩阵C的行向量组与矩阵A的行向量组等价

（B）矩阵C的列向量组与矩阵A的列向量组等价

（C）矩阵C的行向量组与矩阵B的行向量组等价

（D）矩阵C的列向量组与矩阵B的列向量组等价

答案（B）

解析 AB＝C⇒C的列向量组可由A的列向量组线性表示；又B可逆，则CB－1＝A⇒A的列向量组可由C的列向量组线性表示，于是选（B）．