考研数学二矩阵概念、运算及性质

矩阵的概念 矩阵的线性运算 矩阵的乘法 方阵的幂 方阵乘积的行列式 矩阵的转置 逆矩阵的概念和性质 矩阵可逆的充分必要条件 伴随矩阵 矩阵的初等变换 初等矩阵 矩阵的秩 矩阵的等价 分块矩阵及其运算

1．理解矩阵的概念，了解单位矩阵、数量矩阵、对角矩阵、三角矩阵，对称矩阵、反对称矩阵和正交矩阵以及它们的性质．

2．掌握矩阵的线性运算、乘法、转置以及它们的运算规律，了解方阵的幂与方阵乘积的行列式的性质．

3．理解逆矩阵的概念，掌握逆矩阵的性质以及矩阵可逆的充分必要条件．理解伴随矩阵的概念，会用伴随矩阵求逆矩阵．

4．了解矩阵初等变换的概念，了解初等矩阵的性质和矩阵等价的概念，理解矩阵的秩的概念，掌握用初等变换求矩阵的秩和逆矩阵的方法．

5．了解分块矩阵及其运算．

1.矩阵及分块矩阵的基本运算（考点7、8）

这部分的重点是矩阵的乘法运算，如αβT，βαT，ααT，αTβ，βTα，αTα符号之间的区别与联系；方阵的幂、多项式及方阵的行列式是考试热点；要理解矩阵的分块，这对研究一些复杂问题往往起到重大作用，如研究AB＝C之间的线性表示关系．

2.矩阵的逆及伴随矩阵（考点9、10）

这部分的公式比较多，性质相似，要注意作对比几乎是必考公式．

3.初等变换及矩阵的秩（考点11、12）

这部分的引入使得内容丰富而精彩，矩阵的初等变换不要与行列式的性质混淆，要知道什么时候只能作行变换，什么时候可以行列一起作变换（求秩时）；要弄清初等矩阵与初等变换的关系，会熟练应用初等矩阵表示对应的初等变换过程；矩阵的秩是线性代数的核心，要理解秩的概念（非零子式的最高阶数），要会用初等变换求具体矩阵的秩，要会结合秩的诸多性质求抽象矩阵的秩．关于秩的应用将会在后面内容中陆续展开．

考点7 矩阵的定义及运算

1．矩阵的定义

由m×n个数aij排成的m行n列的数表

称为一个m行n列矩阵，简称m×n矩阵，记为A．

行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵．

两个矩阵的行数相等、列数也相等时，称它们是同型矩阵．若A与B是同型矩阵且对应元素相等，即aij＝bij，那么称A与B相等，记作A＝B．

元素都是0的矩阵称为零矩阵，记作O，注意不同型的零矩阵是不相等的．

对于n阶矩阵，主对角线以外的元素都是0的矩阵称为对角矩阵，记作

对于n阶矩阵，主对角线元素都是1，其他元素都是0的矩阵称为单位矩阵，记作

2．矩阵的加法

设有两个同型矩阵A＝［aij］m×n和B＝［bij］m×n，那么矩阵A与B的和记作A＋B，规定为

3．矩阵的数乘

数λ与矩阵Am×n的乘积记作λA，规定为

矩阵加法与数乘矩阵统称为矩阵的线性运算，具有以下性质：

（1）A＋B＝B＋A；

（2）（A＋B）＋C＝A＋（B＋C）；

（3）（λμ）A＝λ（μA）；

（4）（λ＋μ）A＝λA＋μA；

（5）λ（A＋B）＝λA＋λB．

4．矩阵的乘法

设A＝［aij］是m×s矩阵，B＝［bij］是s×n矩阵，矩阵A与矩阵B的乘积是一个m×n矩阵C＝［cij］，其中cij＝ai1b1j＋ai2b2j＋…＋aisbsj（i＝1，2，…，m；j＝1，2，…，n），并记作C＝AB．（实际上，矩阵C的第i行第j列元素cij就是矩阵A的第i行元素与矩阵B的第j列元素两两乘积之和）

一般情况下（可借助下面例1体会）

①AB≠BA，若AB＝BA，则称A与B可交换；

②AB＝O⇒／A＝O或B＝O；

（应该指出，在AB＝O时，若对A或B再附加其他一些条件，可以推出A＝O或B＝O．）

③AB＝AC，A≠O⇒／B＝C．

（应该指出，在AB＝AC时，若A可逆，则B＝C．）

矩阵的乘法具有以下结合律和分配律性质：

（1）（AB）C＝A（BC）；

（2）λ（AB）＝（λA）B＝A（λB）；

（3）A（B＋C）＝AB＋AC，（B＋C）A＝BA＋CA；

（4）AE＝EA＝A；AO＝OA＝O．

①两个对角矩阵乘法的规律就是对角线元素对应相乘；

②两个对角矩阵是可交换的，即Λ1Λ2＝Λ2Λ1．

本题若直接计算，则要作4次乘法，利用运算规律（加法交换律、加法结合律、乘法对加法的分配律）化简后，则只需作两次乘法，运算量减少了一半，可见作矩阵运算时先进行必要的化简是很重要的．这里要注意，化简过程是恒等变形，因此，提取公因子时不能颠倒相乘矩阵的左、右次序．

5．方阵的幂

6．矩阵的转置

把矩阵A的行换成同序数的列得到一个新矩阵，叫作A的转置矩阵，记作AT．称满足AT＝A的矩阵A为对称矩阵；满足AT＝－A的矩阵A为反对称矩阵．

对任意矩阵A，恒有A＋AT，AT A，AAT是对称矩阵，A－AT是反对称矩阵．

矩阵的转置运算具有以下性质：

（1）（AT）T＝A；（2）（A＋B）T＝AT＋BT；（3）（λA）T＝λAT；（4）（AB）T＝BT AT．

特别注意，性质（4）可推广为（A1A2…An）T＝ATn ATn－1…AT2 AT1．

（1）设A，B为n阶矩阵，且A为对称矩阵，证明BT AB也是对称矩阵；

（2）设A，B都是n阶对称矩阵，证明AB是对称矩阵的充要条件是AB＝BA．

证明 （1）（BT AB）T＝BT AT（BT）T＝BT AB（因A为对称矩阵），证毕．

（2）（AB）T＝BT AT＝BA（因A，B都为对称矩阵），故（AB）T＝AB⇔BA＝AB，证毕．

这是一个数，且该数就是方阵αβT或βαT的对角线之和；

这是一个数，且该数就是方阵βαT或αβT的对角线之和；

这是一个数，且该数就是方阵ααT的对角线之和．

αβT，βαT，ααT都是列在前、行在后，其结果都是一个任意两行（列）都成比例的方阵（秩为1），且该方阵三行之比就是左端的列，该方阵三列之比就是右端的行，也就是说秩为1的方阵总可以分解为一列乘一行．βTα，αTβ，αTα都是行在前、列在后，其结果都是一个数．

7．方阵的行列式

由n阶方阵A的元素所构成的行列式（各元素的位置不变），称为方阵A的行列式，记作

方阵的行列式具有以下性质：

（1）

特别注意，

矩阵是由数构成的一种数表，而行列式是按一定运算法则所确定的一个数，数表与数是两个不同的概念．要理解矩阵的概念，注意矩阵与行列式的联系与区别，两者不要混淆．当A≠B时，｜A｜与｜B｜可能相等也可能不相等，由A≠B得不到｜A｜≠｜B｜．

考点8 矩阵的分块

1．矩阵分块的概念

用几条纵线和横线把一个矩阵分成若干小块，每一小块称为原矩阵的子矩阵．把子矩阵看作原矩阵的一个元素，就得到了分块矩阵．

如A以行分块：

式中，αi＝［ai1，ai2，…，ain］是A的一个子矩阵．

B以列分块：

式中，βj＝［b1j，b2j，…，bmj］T是B的一个子矩阵．

2．分块矩阵的运算（假设以下都是可以运算的）

（1）加法运算．

（2）数乘运算．

（3）乘法运算．

（4）转置运算．

3．分块对角矩阵的性质

解 法1 直接计算（留给读者）．

解 法2 分块计算．

设α1，α2，α3均为3维列向量，记矩阵

A＝［α1，α2，α3］，B＝［α1＋α2＋α3，α1＋2α2＋4α3，α1＋3α2＋9α3］，如果｜A｜＝1，那么｜B｜＝__________．

答案2

解析 利用矩阵的性质计算．

本题关键是进行列分块，从而转化成上例的形式．

最后，再通过一个例子进一步阐述分块的思想．

如果AB＝C，其中A是m×n矩阵，B是n×s矩阵，那么对矩阵B，C按行分块有

可见矩阵AB的行向量δ1，δ2，…，δm可由B的行向量β1，β2，…，βn线性表示．

类似地，对矩阵A，C按列分块，有

说明矩阵AB的列向量γ1，γ2，…，γs可由A的列向量α1，α2，…，αn线性表示．

考点9 逆矩阵

1．定义

对于n阶矩阵A，如果有一个n阶矩阵B，使AB＝BA＝E，则称A是可逆的，且把矩阵B称为A的逆矩阵，记为B＝A－1．另外，如果A可逆，那么A的逆矩阵是唯一的．

行列式的各个元素的代数余子式Aij所构成的如下的矩阵

称为矩阵A的伴随矩阵，且有恒等式

设2阶矩阵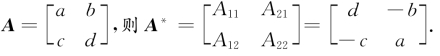（主对调，副变号）

设A，B为n阶矩阵，AB＝A＋B，证明：AB＝BA．

证明 由AB＝A＋B，得AB－A－B＝O，从而有AB－A－B＋E＝E，故

（A－E）（B－E）＝E，

根据上述定理2，有（B－E）（A－E）＝E，即

BA－A－B＝O，

故BA＝A＋B，从而AB＝BA．

设n阶方阵A，B，C满足关系式ABC＝E，其中E是n阶单位矩阵，则必有（ ）．

（A）ACB＝E（B）CBA＝E（C）BAC＝E（D）BCA＝E

答案（D）

解析 因为ABC＝E，即A（BC）＝E，故方阵A与BC互为逆矩阵，从而有（BC）A＝E，即BCA＝E．

实际上，ABC＝E⇔BCA＝E⇔CAB＝E，把A，B，C顺时针围成一圈，任意三者顺时针相乘都等于E．

2．性质

逆矩阵具有以下性质：

3．求法

根据分块对角矩阵求逆矩阵的方法，得

设矩阵A满足A2＋A－4E＝O，其中E为单位矩阵，则（A－E）－1＝__________．

答案

分析 本题考查的是矩阵的简单运算．给出某矩阵方程，来求某矩阵（或其逆矩阵）的表达式，或给出某数字矩阵，来求另一个与此有关的矩阵（或其逆矩阵）的具体答案，是常考题．本题是其中较容易的一种形式．最简单的做法是，将某倍E移到等号右边，左边留下的项应能提出因式A－E．

解析 将原式写成A2＋A－2E＝2E，即（A－E）（A＋2E）＝2E，从而（A－E）－1＝

抽象矩阵求逆，往往都是利用定义法．

设n阶矩阵A满足2A（A－E）＝A3，则（E－A）－1＝__________．

答案 A2－A＋E

解析 由2A （A－E）＝A3，得A3－2A2＋2A＝O，则－A3＋2A2－2A＋E＝E，即（E－A）（A2－A＋）E＝E，故（E－A）－1＝A2－A＋E．

分析 此类填空题，总是先进行符号推导，再代入数字运算．

解析 因为

本题利用了单位矩阵E恒等变形的技巧．

设A，B，A＋B均为n阶可逆矩阵，证明：A－1＋B－1是可逆矩阵，且写出（A－1＋B－1）－1．

分析 本题的题设条件不是一个等式，而且从题设条件也难以构造出一个合适的等式，所以要另找途径．为此，从数的类比运算中去找思路．在数中该题相当于：已知a≠0，b≠0，a＋b≠0，求（a－1＋b－1）－1．这是容易求得的，因

在上述数的求解过程中所用方法是通分，通分实质是把数1看作把这种想法移植到矩阵中来可有如下证法．

证明

因题设B－1，A＋B，A－1均为可逆矩阵，所以B－1（B＋A）A－1为可逆矩阵，即证得A－1＋B－1为可逆矩阵，且

①B－1（B＋A）A－1＝A－1＋B－1是易见的．但反过来要从A－1＋B－1化为B－1（B＋A）A－1是需要技巧的，而这种技巧源于将E看作B－1B或AA－1．(www.xing528.com)

②用类似的方法也可化得

A－1＋B－1＝A－1（A＋B）B－1．

所以说本题的答案也可写为（A－1＋B－1）－1＝B（A＋B）－1A．

③因1阶方阵就是数，所以从数的类比运算中找思路，其实就是先在1阶矩阵中解问题，然后把此种解法的思路推广到n阶矩阵．

设A是n阶矩阵，满足A2－3A＋2E＝O，当A≠E时，判别A－2E是否可逆并说明理由．

解 由A2－3A＋2E＝O，整理得（A－2E）（A－E）＝O，于是A－E的每一列都是方程组（A－2E）x＝0的解（这一点的详细由来可见第四章线性方程组考点16中的例4），又A≠E，故A－E≠O，这表明方程组（A－2E）x＝0有非零解，于是＝0（克拉默法则），故A－2E不可逆．

设A＝E－ξξT，其中E是n阶单位矩阵，ξ是n维非零列向量，ξT是ξ的转置．证明：

（1）A2＝A的充要条件是ξTξ＝1；

（2）当ξTξ＝1时，A是不可逆矩阵．

证明 （1）A2＝（E－ξξT）（E－ξξT）＝E－2ξξT＋ξξTξξT＝E－（2－ξTξ）ξξT．A2＝A⇔E－（2－ξTξ）ξξT＝E－ξξT，即（2－ξTξ）ξξT＝ξξT，亦即（1－ξTξ）ξξT＝O．

因为ξ是非零列向量，故n阶方阵ξξT≠O，即1－ξTξ＝0．故A2＝A的充要条件是1－ξTξ＝0，即ξTξ＝1．

（2）（反证）当ξTξ＝1时，有A2＝A．

若A可逆，则上式两端分别左乘A－1，有

A－1A2＝A－1A＝E，

则

E＝（A－1A）A＝A．

由已知A＝E－ξξT，即ξξT＝O，矛盾．故A是不可逆矩阵．

4．逆矩阵的简单应用

含有未知矩阵的等式称为矩阵方程．矩阵方程的基本形式有三类：

AX＝C，XA＝C，AXB＝C．

若A，B可逆，则其解分别是

X＝A－1C，X＝CA－1，X＝A－1CB－1．

答案E

解析 因为矩阵P可逆，由PA＝BP得A＝P－1BP，那么

考点10 伴随矩阵

1．定义

3．求法

方法一：用定义．先求Aij，再拼成A*．

方法二：用公式．若A可逆，则A*＝

设A，B为n阶方阵，则下列选项中正确的是（ ）．

（A）若A，B都可逆，则A*＋B*一定可逆

（B）若A，B都不可逆，则A*＋B*一定不可逆

（C）若A可逆，但B不可逆，则A*＋B*一定不可逆

（D）以上都不正确

答案（D）

答案256

解析 考虑矩阵运算恒等变形，

答案（A）

解析 由A*＝AT，知｜A*｜＝｜AT｜，而｜A*｜＝｜A｜3－1＝｜A｜2，｜AT｜＝｜A｜，于是｜A｜2＝｜A｜，从而｜A｜＝1或0；另一方面，由A*＝AT，还可知aij＝Aij（i，j＝1，2，3），按第一行对｜A｜展开，有

从而｜A｜＝1，再由

答案（D）

解 法1 因A，B不知道是否可逆，故可对四个选项依次根据题设计算与C的乘积，检验矩阵C与哪个选项的乘积等于｜C｜E＝｜A｜｜B｜E．对选项（D），有

答案0

解析 显然｜A｜＝1≠0，A可逆，求A－1（用初等变换法），得

考点11 矩阵的初等变换

下面三种变换称为矩阵的初等变换：

（1）互换两行（列）；

（2）以数k≠0乘某一行（列）的所有元素；

（3）把某一行（列）的k倍加到另一行（列）对应元素上．

如果矩阵A经过有限次初等变换变成矩阵B，则称A与B等价．

A与B等价⇔存在可逆矩阵P和Q，使PAQ＝B⇔A与B同型且r（A）＝r（B）．

零行元素（如果有的话）在最底行，每行左起第一个非零元素所在列下方元素全是0，称这种矩阵为行阶梯形矩阵；进一步如果每行左起第一个非零元素是1，且它所在列其他元素全是0，则称这种矩阵为行最简形矩阵．

对于任何非零矩阵，总可经过有限次初等行变换把它变为行阶梯形矩阵和行最简形矩阵．

由单位矩阵E经过一次初等变换得到的矩阵P称为初等矩阵．

初等矩阵具有以下性质：

（1）初等矩阵P左（右）乘A，所得PA（AP）就是对矩阵A作了一次与P同样的初等行（列）变换．（这里“与P同样的初等行（列）变换”是指由单位矩阵E变成初等矩阵P时所用的变换）

（2）初等矩阵都是可逆的，且其逆仍是同类型的初等矩阵，即

（3）若A可逆，则A可写成若干初等矩阵乘积的形式，即A＝P1P2…Ps，这里Pi（i＝1，2，…，s）都是初等矩阵．

则必有（ ）．

（A）AP1P2＝B （B）AP2P1＝B

（C）P1P2A＝B （D）P2P1A＝B

答案（C）

解析 矩阵B可以看作由矩阵A依次进行下列两次初等行变换得到的：先把A的第1行加到第3行上，再把所得矩阵的1，2两行互换．这两次初等变换对应的初等矩阵分别为矩阵P2和P1，于是由“对矩阵A作初等行变换相当于初等矩阵左乘A”，即知（C）正确．

例3 设A为3阶矩阵，将A的第2列加到第1列得矩阵B，再交换B的第2行与第3行得单位矩阵．记则A＝（ ）．

（A）P1P2（B）

（C）P2P1（D）

答案（A）

解析 对矩阵P作一次初等列变换：把第2列加到第1列上，便可得到矩阵Q，则Q＝PE21（1），其中

设A是n阶（n≥2）可逆矩阵，交换A的第1行与第2行得B，则（ ）．

（A）交换A*的第1列与第2列得B*

（B）交换A*的第1行与第2行得B*

（C）交换A*的第1列与第2列得－B*

（D）交换A*的第1行与第2行得－B*

答案（C）

解析 由题设知B＝E12A，其中E12是将矩阵第1行（列）与第2行（列）交换的初等变换所对应的初等矩阵，因而有

由于

且｜B｜＝－｜A｜，所以

而E12右乘A*，即将A*的第1列与第2列交换．因而选项（C）是正确的．

考点12 矩阵的秩

在m×n矩阵A中，任取k行与k列（k≤m，k≤n），位于这些行列交叉处的k2个元素，不改变它们在A中所处的位置次序而得到的k阶行列式，称为矩阵A的k阶子式；A中非零子式的最高阶数称为矩阵A的秩，记作r（A），规定零矩阵的秩为0．

r（A）＝r⇔A中有r阶子式不为0，而所有r＋1阶子式全为0；

r（A）＜3⇔A中所有3阶子式全为0；

r（A）≥2⇔A中有2阶子式不为0．

由秩的定义容易得到以下基本结论：

（1）An×n可逆

初等变换不改变矩阵的秩；行阶梯形矩阵的秩等于其非零行数．

矩阵的秩具有以下性质：

（1）0≤r（Am×n）≤min｛m，n｝；

（2）r （kA）＝r（A）（k≠0）；

（3）r（AB）≤min｛r（A），r（B）｝；

（4）若A可逆，则r（AB）＝r（B），r（BA）＝r（B）；

（5）r （A＋B）≤r（A）＋r（B）；

（6）若Am×n Bn×s＝O，则r（A）＋r（B）≤n；

（7）r（A）＝r（AT）＝r（AT A ）＝r（AAT）；

（8）r （A）*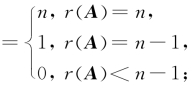

（9）r（A）＝1⇔A＝αβT，其中α，β都是非零列向量．

设A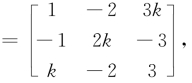问k为何值时，可使

①r（A）＝1；②r（A）＝2；③r（A）＝3．

解 法1 于是①当k＝1时，r（A）＝1；②当k＝－2时，r（A）＝2；③当k≠1且k≠－2时，r（A）＝3．

解 法2 因A是3阶方阵，故所以当k≠1且k≠－2时，r（A）＝3；当k＝－2时，r（A）≤2，又此时A中存在2阶子式

故r（A）≥2，于是r（A）＝2；

当k＝1时，A的各行之间成比例，于是r（A）＝1．

设A为m×n矩阵，B为n×m矩阵，若AB＝E，则（ ）．

（A） r（A）＝m，r（B）＝m（B） r（A）＝m，r（B）＝n

（C） r（A）＝n，r（B）＝m（D） r（A）＝n，r（B）＝n

答案（A）

解析 由已知可得r（A）≤min｛m，n｝≤m，r（B）≤min｛m，n｝≤m．

又m＝r（E）＝r（AB）≤min｛r（A），r（B）｝，即有r（A）≥m及r（B）≥m．所以r（A）＝r（B）＝m，应选（A）．

设A是4×3矩阵，且r（A）＝2，而

答案2

解析 因为B可逆，所以

r（AB）＝r（A）＝2．

设A，B为n阶矩阵，［X Y］表示分块矩阵，则（ ）．

（A）r（［A AB］）＝r（A）（B）r（［A BA］）＝r（A）

（C）r（［A B］）＝max｛r（A），r（B）｝（D）r（［A B］）＝r（［AT BT］）

答案（A）

解 法1一方面，A是［A AB］的子矩阵，因此r（［A AB］）≥r（A）．

另一方面，［A AB］＝A［E B］，因此r（［A AB］）≤r（A），故r（［A AB］）＝r（A）．

解 法2设C＝AB，则C的列向量可由A的列向量线性表示，所以r（［A AB］）＝r（［A C］）＝r（A），选（A）．

设3阶非零矩阵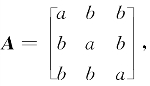若A的伴随矩阵的秩等于1，则必有（ ）．

（A）a＝b或a＋2b＝0（B）a＝b或a＋2b≠0（C）a≠b且a＋2b＝0（D）a≠b且a＋2b≠0

答案（C）

解析

所以a＝b或a＋2b＝0．若a＝b，则r（A）＝1，有r（A*）＝0，不符合题意．故a≠b，且a＋2b＝0．本题应选（C）．

设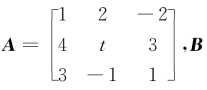为3阶非零矩阵，且AB＝O，则t＝__________．

答案－3

解析 由B≠O，知r（B）≥1，又AB＝O，则r（A）＋r（B）≤3，于是r（A）≤2＜3，故

设A是n阶矩阵，且A2＝E，证明：r（A＋E）＋r（A－E）＝n．

证明 由A2＝E，得A2－E＝O，即（A－E）（A＋E）＝O，故

r（A－E）＋r（A＋E）≤n．