多元函数的概念 二元函数的几何意义 二元函数的极限与连续的概念 有界闭区域上二元连续函数的性质 多元函数的偏导数和全微分 多元复合函数、隐函数的求导法 二阶偏导数 多元函数的极值和条件极值、最大值和最小值
1．了解多元函数的概念，了解二元函数的几何意义．
2．了解二元函数的极限与连续的概念，了解有界闭区域上二元连续函数的性质．
3．了解多元函数偏导数与全微分的概念，会求多元复合函数一阶、二阶偏导数，会求全微分，了解隐函数存在定理，会求多元隐函数的偏导数．
4．了解多元函数极值和条件极值的概念，掌握多元函数极值存在的必要条件，了解二元函数极值存在的充分条件，会求二元函数的极值，会用拉格朗日乘数法求条件极值，会求简单多元函数的最大值和最小值，并会解决一些简单的应用问题．
1.理论部分（考点46-48）
这部分主要是一元微分概念的推广，重点是偏导数与全微分．
2.计算部分（考点49、50）
这部分主要围绕复合函数及隐函数展开，考查一阶及二阶偏导数的计算，只要弄清原理、认真计算，应当都能过关．
3.应用部分（考点51）
这部分是本章解答题的热点，要注意无条件极值与条件极值的区别，有的题目还需要自己提炼成条件极值，这一点需要注意．
考点46 二元函数的极限及连续
1．二元函数
设D是平面上的一个区域，如果∀（x，y）∈D，变量z按照一定的法则f总有唯一确定的值和它对应，则称z是变量x，y的二元函数，记为z＝f（x，y），其中D称为f（x，y）的定义域，x，y称为自变量，z称为因变量．
二元函数z＝f（x，y）的图形在空间坐标系上是一张曲面．
二元函数的定义域，一般是由一条或几条曲线所围成的平面区域，围成区域的曲线称为区域的边界．
区域可分为如下两类．
①无界区域和有界区域．
无界区域：可伸展到无限远处的区域．
有界区域：总可以被包围在一个以原点为中心、半径适当大的圆内的区域．
②开区域和闭区域．
开区域：不包括任何边界点的区域．
闭区域：包括全部边界在内的区域．
点P（x0，y0）的δ邻域：满足不等式
的点的全体．
点P（x0，y0）的δ去心邻域：满足不等式
的点的全体．
与一元函数一样，二元函数的表示法也只与函数的定义域和对应关系有关，而与用什么字母表示变量符号无关．此种特性常用来求f（x，y）的表达式．
2．二重极限
3．二元函数的连续性
其值随k的取值不同而不同，故极限不存在，从而（0，0）为函数f（x，y）的间断点．
考点47 偏导数
1．偏导数的定义
求分段函数在分段点处的偏导数一般用定义求．
由本题可知，对多元函数来说，函数连续与偏导数的存在之间没有必然联系．出现这种情况，主要原因是二元函数的偏导数起不到一元函数导数的作用，因为偏导数f′x（x0，y0）与f′y（x0，y0）存在只能表明点P（x，y）沿平行于坐标轴方向趋于点P0（x0，y0）时函数变化的情况，不能表示函数沿其他方向的变化情况．而函数在点P0（x0，y0）处连续是一个与P0（x0，y0）邻域有关的概念，即不仅要考虑邻域内平行于x轴、y轴方向上各点处函数值的变化趋向，还要考虑整个邻域内（仅f（x，y）有定义的）其他点上函数值的变化趋向，亦即要考虑点P（x，y）以各种方式沿所有方向趋于点P0（x0，y0）的情况．而函数在一点处的偏导数一般是不能全面反映出函数在这点的变化情况的，因而出现“二元函数在某点两个偏导数存在，但它在该点不连续”这种现象是不难理解的．
2．高阶偏导数
设z＝f（x，y），根据求导次序的不同，二阶偏导数有以下4个：
若f′x（x，y），f′y（x，y）在区域D上为零，证明f（x，y）在区域D上为常数．
证明 设（x0，y0），（x，y）为区域D上任意两点，令x＝x0＋Δx，y＝y0＋Δy，则
考点48 全微分(www.xing528.com)
1．全微分的定义
（2）充分条件．
（1）证明f（x，y）在点（0，0）处不连续；
（2）求f′x（0，0），f′y（0，0）；
（3）讨论f′x（x，y）在点（0，0）处的连续性．
3．可微的判定方法
考点49 复合函数的偏导数与全微分
1．链式求导法则
像本题这样多层f的复合在求导过程中（尤其涉及代值时）不要用平时惯用的简写形式：f′1，f″12，…，因为f′1［x，f（x，x）］与f′1（x，x）含义是不一样的．
设f（x，y）具有二阶连续偏导数，且f″11（x，2x）＝f″22（x，2x），f（x，2x）＝x2，f′1 （x，2x）＝x．求f″11 （x，2x）与f″12 （x，2x）．
解 对等式f（x，2x）＝x2两端关于x求导得
f′1（x，2x）＋2f′2（x，2x）＝2x，
再对x求导得
f″11（x，2x）＋2f″12（x，2x）＋2f″21（x，2x）＋4f″22（x，2x）＝2，
结合题设有5f″11（x，2x）＋4f″12（x，2x）＝2．对于等式f′1（x，2x）＝x两端再对x求导得
f″11（x，2x）＋2f″12（x，2x）＝1，
于是
2．偏导数的变量代换
（1）由方程组①解出反函数组
（2）先求出因变量z对旧自变量x，y的偏导数，将新自变量u，v视为中间变量，利用链式法则求出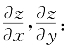
解 这类题有两种思路构造复合关系：
由于题中给出的是z关于x，y的偏导数的方程，采用后一种复合关系，求出
代入所给方程化简，较为方便．
考点50 隐函数的偏导数及全微分
由复合函数求导公式，有
考点51 极值及最值
1．极值的定义
类型一：二元显函数
类型二：二元隐函数
3．条件极值
（3）解上述方程组．
（注意，这里解出的点只能说是可能的极值点，但考试考的基本都是最值点，这种情况下我们自然就不必再纠结这些点究竟是不是极值点了）
（4）比较以上函数值大小．
有时目标函数比较复杂，为简便计算试着把目标函数等价转化，如本题由d转化成d 2．
4．闭区域上的最值
求连续函数z＝f（x，y）在有界闭区域D上的最值．
（1）求f（x，y）在D内部的偏导数为0和偏导数不存在的点；
（2）求f（x，y）在D的边界上的最值点，即拉格朗日函数F（x，y，λ）的偏导数为0的点；
（3）比较上述各函数值的大小，最大的为最大值，最小的为最小值．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
