岩缝扩缝效应分析及布辛涅斯克方程估算

这里谈的压力扩缝，容易与上节谈的水力劈裂相混淆。因为二者所产生的效果都是扩开裂缝。为了区别它们，现分别给以定义。

水力劈裂：是指在向钻孔内压入流体时，由扩张应力引起的在钻孔孔壁上产生的新裂缝和在原有裂缝上产生的裂缝再扩展。由此导致的岩体变形，既包括有可以回复的弹性变形，也包括不能回复的塑性变形。

压力扩缝：是指由于流体在缝隙内流动给两壁岩体以压缩应力，而引起的裂缝宽度在原有基础上进一步扩宽的值，此种扩宽仅是由于岩体的弹性变形产生的。

液体因受压力的驱使进入岩缝和在其中流动，将同时给缝的两壁以压缩应力。此压缩应力将引起岩缝宽度进一步扩展。扩展的数值，大都按照布辛涅斯克方程进行估算。该公式是假定在一个圆形体内，由弹性材料夹持的缝面上因承受均匀荷载而引起弹性变形（图10-4）。萨巴利（1969）认为这假定比较接近于对片状裂隙呈辐射状灌注时的情况。但实际上，缝面上承受的压力是不相等的，而是向外越来越小，如图10-5所示。另外，实际缝面很少是均匀展布的，因此，应将由此公式算出的数值看作是近似的。布辛涅斯克公式分别给出了承载面中心、流体波及面前缘处的变形量［1］；

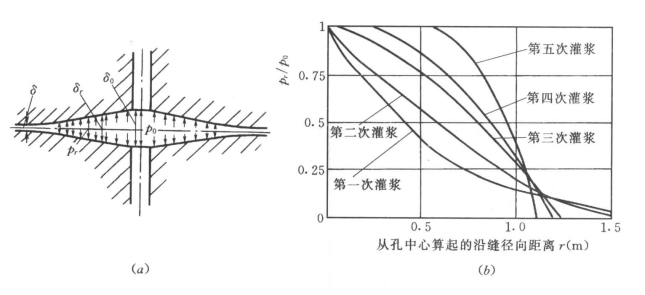
图10-4　沿裂缝的变形和压力分布特征

（a）承受均匀压力pa时裂缝的变形（根据萨巴列，1960年）；（b）压力沿裂缝的分布（根据豪斯比，1939年）

式中　E、μ——分别为岩石的弹性模量和泊松比；(www.xing528.com)

　　　R——扩散半径；

　　　Pa——作用于缝面上的平均压力。

按照式（10-13）和式（10-14），当E为104MPa、μ为0.25、Pa为1MPa时，在对片状裂隙呈辐射状扩散压水或灌浆，当液体扩散到距离钻孔中心1m处所引起的裂缝扩宽为

当浆液波及到2m处，为

不难理解，这个结果，将对压水试验所得成果和灌浆效果产生重大影响。